miniMitts27
- 3
- 0
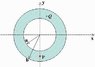
Given a spherical shell insulator as defined by an inner radius a = 4 cm and an outer radius b = 6 cm and carries a total charge of Q = + 9 C (1 C = 10-6 C). (You may assume that the charge is distributed uniformly throughout the volume of the insulator).
What is Ey, the y-component of the electric field at point P which is located at (x,y) = (0, -5 cm)? (picture of situation is attached)
Basically I just don't even know where to start. I realize that it's a Gauss' Law problem... I just don't know where to go from here. Any help would be greatly appreciated!
What is Ey, the y-component of the electric field at point P which is located at (x,y) = (0, -5 cm)? (picture of situation is attached)
Basically I just don't even know where to start. I realize that it's a Gauss' Law problem... I just don't know where to go from here. Any help would be greatly appreciated!