General Relativity Basics: The Principle of Equivalence

[JDoolin]

However, notice that we have established that the rindler coordinates also has a nonzero dg/dx, since the born rigid system must have different accelerations at different ruler distances.

Actually, what we established was that there was a nonzero dg/dX when g was based on the acceleration in the inertial frame. But because the rate of proper time \tau is different at those different x values, this means that in the accelerated frame, the local value of g is also different at those different x values.

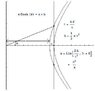
Instead of

g(x)=\frac{d^2 X_{rocketfloor}}{d T_{inertialclock}^2}​

we want:

g(x)=\frac{d^2 x_{inertialobject}}{d \tau_{rocketclock}^2}​

Not quite. It's true that, for the particular case we're considering, the Schwarzschild spacetime outside a gravitating body, the tidal gravity happens to equal dg/dr; but that's not true in general, and the fact that dg/dx is also nonzero in Rindler coordinates does not mean that there is nonzero tidal gravity in flat spacetime (which is what Rindler coordinates apply to).

Whether we claim zero tidal gravity, or not, I think it is important to explicitly define our variables. In the rindler coordinates, neither dg/dr, nor dg/dx are sufficient, because g is a function of the local rate of time.

The general rule is that "tidal gravity" is just another name for "spacetime curvature"; so tidal gravity is only nonzero if spacetime is curved, which it is outside a gravitating body, but is not (obviously) in flat spacetime, even for accelerating observers.

I thought it was obvous that spacetime was flat, even for accelerating observers, but now we have this nonzero dg/dX in the inertial frame which means it is no longer obvious that dg/dx is zero in the accelerated frame.

 

[PeterDonis]

I thought it was obvous that spacetime was flat, even for accelerating observers, but now we have this nonzero dg/dX in the inertial frame which means it is no longer obvious that dg/dx is zero in the accelerated frame.

I think it will indeed turn out when you do the computation you describe in post #59 that dg/dx will *not* be zero in the accelerated frame. The reason is simple: observers at different Rindler coordinates x certainly *feel* different accelerations, and that's what the function g(x) is supposed to capture--the acceleration that an observer at a given x *feels* (would measure with an accelerometer, etc.). So I expect g to vary with x.

But even assuming this is true, as I said before, it does *not* mean that the spacetime is curved. You can't change flat spacetime to curved spacetime by changing your coordinate system (or your state of motion); whether spacetime is flat or curved is a geometric invariant, just like the curvature of the Earth's surface. If you want, we can verify this by explicitly computing the components of the Riemann tensor in Rindler coordinates and verifying that they are all zero (or maybe a kind soul will point us to someplace where that computation has already been done).

 

[JDoolin]

I think it will indeed turn out when you do the computation you describe in post #59 that dg/dx will *not* be zero in the accelerated frame. The reason is simple: observers at different Rindler coordinates x certainly *feel* different accelerations, and that's what the function g(x) is supposed to capture--the acceleration that an observer at a given x *feels* (would measure with an accelerometer, etc.). So I expect g to vary with x.

I think I have a possible approach to the problem, somewhat inspired by your earlier reference to Misner Thorne Wheeler. To find the "gravity" measured by occupants of the rocket at any given x, we can use a diagram similar to the one attached, and use

(x_2 - x_1) = \frac{1}{2} a \tau ^2

I think that \tau is fully determined by x₁ and \Delta x, so we should be able to find an explicit value of a for any given x.

But even assuming this is true, as I said before, it does *not* mean that the spacetime is curved. You can't change flat spacetime to curved spacetime by changing your coordinate system (or your state of motion); whether spacetime is flat or curved is a geometric invariant, just like the curvature of the Earth's surface. If you want, we can verify this by explicitly computing the components of the Riemann tensor in Rindler coordinates and verifying that they are all zero (or maybe a kind soul will point us to someplace where that computation has already been done).

That would be fine, I suppose, with the caveat that I'm effectively tensor illiterate. I got an MS degree in math and physics, but none of my professors ever talked about tensors. PS, I have looked at a few of the Susskind lectures on YouTube, and I am at least skimming MTW, and Wald now, but so far, it's all a little too abstract for me.

 

[SinghRP]

Newtonian equation motion in a gravitational field, written in full:

(Inertial mass) * (Acceleration) = (Intensity of gravitational field) * (Gravitational mass).

It is only when there is numerical equality between the inertial and gravitational mass that the acceleration is independent of the nature of the body. This is the Principle of Equivalence, which has double meanings.
Reference: The Meaning of Relativity, Albert Einstein.

 

[Mentz114]

That would be fine, I suppose, with the caveat that I'm effectively tensor illiterate.

You don't have to be. You understand the concept of spacetime and the geometric invariant ds². All that's needed is to make the leap to curved spacetime, where one *must* use covariant *and* contravariant components to define a geometric invariant.

I tried to explain this in post#9 and #11 in this thread https://www.physicsforums.com/showthread.php?t=431843

Do dimensional indexes throw you, i.e. writing t as x⁰, x as x¹, y as x² and so on ? Or the summation convention x^ax_a=x⁰x₀+x¹x₁+x²x₂+x³x₃ ?

If you hate all the indices try the diff. geom. approach.

 

[SinghRP]

I read discussions under General Physics, Classical Physics, and Specia Relativityl & General Relativity. I THINK there are several slightly varying interpretations of mass, force, accelaration, gravity, etc.

Gamow's One, Two, Three, Infinity raised my curiosity well enough to help me decide to become a physicist. Universities turned me into a marching physicist. Wigner's Symmetries and Reflections made me a humble physicist. I strongly recommend Wigner's essays. What an insigthful book!

 

[JDoolin]

I think it will indeed turn out when you do the computation you describe in post #59 that dg/dx will *not* be zero in the accelerated frame. The reason is simple: observers at different Rindler coordinates x certainly *feel* different accelerations, and that's what the function g(x) is supposed to capture--the acceleration that an observer at a given x *feels* (would measure with an accelerometer, etc.). So I expect g to vary with x.

Well, I think I've come to a conclusion; right now, the result seems surprising to me, but probably won't to you.

\begin{matrix}<br /> x cosh(\phi)=x+h \\<br /> \phi=arccosh\left ( \frac{x+h}{x}\right )\\<br /> \Delta \tau = \frac{x \phi}{c}\\<br /> a = \frac{2 h}{\Delta \tau^2}\\<br /> a=\lim_{h \to 0}\frac{2 h c^2}{x^2 ArcCosh^2(\frac{x+h}{x})}=c^2/x<br /> \end{matrix}​

(The attached diagram might help.)

It comes out so whether you do the calculation by (X and T) or by (x and \tau), you get the very same result for the acceleration.

 

[SinghRP]

General relativity has it that the spacetime continuum is curved. The physics of continuum is dealt with [stress] tensors.
My questions:
(1) The presence of a mass creates the curvature. By how?
(2) If the curvature due to matter is positive, is the sign due to antimatter negative?
(3) Do other fundamental interactions (the strong, the weak, and electromagnetic) create curvatures in their respective fields?

 

[Mentz114]

General relativity has it that the spacetime continuum is curved. The physics of continuum is dealt with [stress] tensors.
My questions:
(1) The presence of a mass creates the curvature. By how?
(2) If the curvature due to matter is positive, is the sign due to antimatter negative?
(3) Do other fundamental interactions (the strong, the weak, and electromagnetic) create curvatures in their respective fields?

Do you want to start another topic with these questions - you are hijacking someone else's topic.

 

[JDoolin]

You don't have to be. You understand the concept of spacetime and the geometric invariant ds². All that's needed is to make the leap to curved spacetime, where one *must* use covariant *and* contravariant components to define a geometric invariant.

I tried to explain this in post#9 and #11 in this thread https://www.physicsforums.com/showthread.php?t=431843

Do dimensional indexes throw you, i.e. writing t as x⁰, x as x¹, y as x² and so on ? Or the summation convention x^ax_a=x⁰x₀+x¹x₁+x²x₂+x³x₃ ?

If you hate all the indices try the diff. geom. approach.

I posted a reply (post 13) there in the other thread; yes I still want to understand tensors.

 

[PeterDonis]

It comes out so whether you do the calculation by (X and T) or by (x and \tau), you get the very same result for the acceleration.

This looks OK to me as a calculation of the acceleration (or rather a verification that the calculation gives the same results in the inertial frame and the accelerated frame). I assume you would then just take the derivative with respect to x to get dg/dx?

 

[JDoolin]

This looks OK to me as a calculation of the acceleration (or rather a verification that the calculation gives the same results in the inertial frame and the accelerated frame). I assume you would then just take the derivative with respect to x to get dg/dx?

Yes. I think that comes out to be

\frac{dg}{dx}=-\frac{c^2}{x^2}.​

http://groups.google.com/group/sci.physics.relativity/msg/6ff91383c387f7a1?hl=en" tidal gravity as a "divergence of free-fall paths." So is dg/dx the definition of tidal gravity? Could it be that what we have here is the divergence of free-fall paths caused by Lorentz contraction alone?

 

[PeterDonis]

URL="http://groups.google.com/group/sci.physics.relativity/msg/6ff91383c387f7a1?hl=en"]Daryl McCullough describes[/URL] tidal gravity as a "divergence of free-fall paths." So is dg/dx the definition of tidal gravity? Could it be that what we have here is the divergence of free-fall paths caused by Lorentz contraction alone?

No. The *free-fall paths* are not diverging; the *accelerated* paths are (actually, they're "converging" from the point of view of the global inertial frame, but converging is just "negative diverging", so to speak). The free-fall paths remain parallel (this is obvious in the global inertial frame); they don't converge or diverge. Hence, the tidal gravity is zero.

In the spacetime around the gravitating body, on the other hand, the actual free-fall paths converge or diverge; which they do depends on their relative orientation. For example, two free-fall paths separated radially will diverge (their separation will increase with time), while two free-fall paths separated tangentially will converge (their separation will decrease with time).

I realize that, as it stands, the above may not be very enlightening, because "separation", as it stands, is frame-dependent. After all, the accelerated observers see their own separations as constant, whereas inertial observers (in the flat-spacetime scenario, at least) see their separations as decreasing with time (due to Lorentz contraction). However, it turns out that there *is* an invariant way to define "separation" for *nearby* geodesics (free-falling paths): pick one free-falling path as the "origin" or "reference worldline", and construct a local inertial frame around it. Then the "separation" between the two free-falling paths is just the spatial distance between them in the local inertial frame, and the *change* in the separation is the derivative of that spatial distance with respect to proper time along the reference worldline. (Note that in curved spacetime, a "local" inertial frame must be "local" in time as well as in space, so actually, we have to construct a separate local inertial frame and go through the above procedure at each *event* on the reference worldline.)

If we do this for the accelerated paths in flat spacetime (the "Rindler worldlines"), we find that the "separation" x in Rindler coordinates does *not* meet the above requirements, so we can't use it to measure the "separation" we need to evaluate tidal gravity. Instead, we have to look at the free-falling worldlines themselves and construct local inertial frames around them. Of course in this particular case that's easy, because all of them are just the worldlines of objects at rest in the global inertial frame, which therefore qualifies as the "local inertial frame" for all of them (with the origin shifted appropriately, if you want to be precise), and all of them obviously maintain constant separation in that frame. So there's no tidal gravity.

In the curved spacetime around a gravitating body, on the other hand, we have to go through the full procedure I described above, and when we do, we find that the separations of nearby free-falling worldlines *do* converge or diverge as I stated above.

The technical term for the math behind the procedure I described above is "equation of geodesic deviation"; the sections on that subject in MTW or Wald are decent places to start if you want to study it further. However, their treatment requires full-blown tensor algebra. If I can find a discussion that's more oriented towards the physical aspects I'll post a link.

 

[JDoolin]

The *free-fall paths* are not diverging; the *accelerated* paths are (actually, they're "converging" from the point of view of the global inertial frame, but converging is just "negative diverging", so to speak).

I can't tell whether you are disagreeing with the physics, or just the words I am using.

Two stationary particles in the inertial frame will appear, in the rocket frame, to rise up from below, decelerating, and spreading out until they stop. Then they will appear to fall down, accelerating and contracting. Both the apparent spreading out, and the contracting are mathematically identical to what one would expect from Lorentz Contraction of a ruler placed between the two objects.

Do you disagree with this?

Edit: With one extra caveat--the top and bottom of any free-falling object will appear to be moving at different velocities. In general Lorentz Transformation alone means the front and back are moving at the same velocity

 

[JDoolin]

Then the "separation" between the two free-falling paths is just the spatial distance between them in the local inertial frame, and the *change* in the separation is the derivative of that spatial distance with respect to proper time along the reference worldline. (Note that in curved spacetime, a "local" inertial frame must be "local" in time as well as in space, so actually, we have to construct a separate local inertial frame and go through the above procedure at each *event* on the reference worldline.)

If we do this for the accelerated paths in flat spacetime (the "Rindler worldlines"), we find that the "separation" x in Rindler coordinates does *not* meet the above requirements, so we can't use it to measure the "separation" we need to evaluate tidal gravity.

I didn't understand the above requirements. When you say "the local inertial reference frame" are you referring to the momentarily comoving reference frame of the accelerating body? Of course that quantity doesn't change. That's kind of the point of Lorentz Contraction.

Possibly, we are talking about two different x's. You are talking about x's being drawn up on the side of the rocket-ship. I'm talking about the x coordinate of a free-falling body, as measured by the ruler drawn up on the side of the rocket ship.

 

[PeterDonis]

I can't tell whether you are disagreeing with the physics, or just the words I am using.

Two stationary particles in the inertial frame will appear, in the rocket frame, to rise up from below, decelerating, and spreading out until they stop. Then they will appear to fall down, accelerating and contracting. Both the apparent spreading out, and the contracting are mathematically identical to what one would expect from Lorentz Contraction of a ruler placed between the two objects.

Do you disagree with this?

Edit: With one extra caveat--the top and bottom of any free-falling object will appear to be moving at different velocities. In general Lorentz Transformation alone means the front and back are moving at the same velocity

I don't disagree with the physics, but I do say that what you've described above is not "tidal gravity". The apparent spreading out and contracting in the rocket frame are, as you note, kinematic effects; we can transform them away by switching to the global inertial frame. Tidal gravity can't be transformed away by changing reference frames. See my next post responding to your next post.

 

[PeterDonis]

I didn't understand the above requirements. When you say "the local inertial reference frame" are you referring to the momentarily comoving reference frame of the accelerating body?

Sort of. The key thing is that, to measure geodesic deviation, you have to compare two nearby geodesics, and the worldline of an accelerating observer is not a geodesic. In the MCIF anywhere along the accelerating observer's worldline, you can pick two nearby geodesics and look at whether they converge or diverge as judged from the MCIF; but in doing that, you will have to look beyond the "momentarily comoving" part of the MCIF, because if you restrict yourself to the "momentarily comoving" part only, it by definition is too small to see tidal effects!

In the particular case we're discussing, suppose we pick the MCIF of the rocket at the instant when one free-falling object is momentarily at rest relative to the rocket (and at the same spatial point). That MCIF will then be the same as the rest frame of the free-falling object (which, since spacetime is flat in this scenario, is basically the global inertial frame), but it will only be "momentarily comoving" with the rocket in a very small patch surrounding the instant when the two objects are momentarily at rest relative to each other. Within that small patch, we can't tell if the spacetime is flat or curved (i.e., whether there are or are not tidal effects); but outside that patch, we can see that, in the inertial frame, the two free-falling objects maintain constant separation for all time, so there's no tidal gravity. We can't use their changing separation in the rocket frame for this purpose because the rocket frame doesn't "stay inertial" outside the small patch.

In the corresponding case in curved spacetime, if we again chose our MCIF the same way, the inertial frame of the free-falling object, *extended outside the small momentarily comoving patch*, would be our "local inertial frame" for measuring geodesic deviation. Then we would see that, *outside* the small momentarily comoving patch, the separation of the other nearby free-falling object would *not* remain constant--it would converge or diverge (depending on the direction of the separation), even as judged from the inertial frame. This is not a kinematic effect; it's a real, invariant convergence or divergence of the geodesics and can't be transformed away by changing reference frames.

 

[yuiop]

In the spacetime around the gravitating body, on the other hand, the actual free-fall paths converge or diverge; which they do depends on their relative orientation. For example, two free-fall paths separated radially will diverge (their separation will increase with time), while two free-fall paths separated tangentially will converge (their separation will decrease with time).

In the attached diagram I have plotted some worldlines of free falling particles (blue lines) near the event horizon in Schwarzschild coordinates. In these coordinates the particles seem to be initially diverging radially but as they approach the event horizon (vertical green line at r = 2m =1) they converge radially. (The red lines are the Fermi normal lines of the primary free falling observer which is indicated by the black boxes at the intersections.)

Are you saying that in the free falling frame the particles will appear to continue diverging according to the free falling observer as they approach and pass through the event horizon? It would be nice is someone could plot the free falling wordlines from the point of view of the free falling observer to prove that is the case.

 

[yuiop]

Are you saying that in the free falling frame the particles will appear to continue diverging according to the free falling observer as they approach and pass through the event horizon?

O.K. I think I have answered my own question. I have managed to plot the the worldlines of free falling observers (blue curves) in Gullstrand-Painleve coordinates in the attached diagram and they do indeed appear to diverge continuously as the event horizon is approached and continue to diverge after passing through the event horizon from the point of view of the free falling GP observers.

The green curves are ingoing null paths and the red curves are outgoing null paths. The event horizon is at x=2 in the diagram.
It can also be seen from the way the null paths have been plotted, that the radar distance between neighbouring free falling observers is continuously increasing as they fall.

If anyone wants the equations to plot these curves, just ask

 

[Passionflower]

O.K. I think I have answered my own question. I have managed to plot the the worldlines of free falling observers (blue curves) in Gullstrand-Painleve coordinates in the attached diagram and they do indeed appear to diverge continuously as the event horizon is approached and continue to diverge after passing through the event horizon from the point of view of the free falling GP observers.

The green curves are ingoing null paths and the red curves are outgoing null paths. The event horizon is at x=2 in the diagram.
It can also be seen from the way the null paths have been plotted, that the radar distance between neighbouring free falling observers is continuously increasing as they fall.

If anyone wants the equations to plot these curves, just ask

Yes, the equations would be nice. Plots (and even better animated plots) are extremely useful to get a quick overview of what an equation 'does'. In this day and age we have wonderful tools to visualize information and demonstrating something with a plot is an excellent means.

 

[Mentz114]

Are you saying that in the free falling frame the particles will appear to continue diverging according to the free falling observer as they approach and pass through the event horizon? It would be nice is someone could plot the free falling wordlines from the point of view of the free falling observer to prove that is the case.

There is no horizon at r=2m in the Painleve chart.
The metric is

\begin{align*}<br /> \left[ \begin{array}{cccc}<br /> \frac{2\,M}{r}-1 &amp; -\sqrt{\frac{2M}{r}} &amp; 0 &amp; 0\\<br /> -\sqrt{\frac{2M}{r}} &amp; 1 &amp; 0 &amp; 0\\<br /> 0 &amp; 0 &amp; {r}^{2} &amp; 0\\<br /> 0 &amp; 0 &amp; 0 &amp; {r}^{2}\,{sin\left( \theta\right) }^{2} \end{array} \right]<br /> \end{align*}<br />
Note the flat spatial sections.

An observer at rest wrt to the 'rain', will see tidal tensor with T_{rr}=2m/r^3,T_{\theta\theta}=T_{\phi\phi}=-m/r^3

 

[PeterDonis]

There is no horizon at r=2m in the Painleve chart.

This is not correct. The horizon is a frame-independent, invariant feature of the geometry, and it's there regardless of what coordinate chart you use. Yes, the spatial sections in the Painleve chart are flat, but that doesn't mean an observer at r < 2m can send signals to r > 2m. The curvature of the spacetime that makes that impossible is all in the "time dimension" (so to speak) in the Painleve chart, but it's still there.

Edit: Maybe what you meant to say is that there is no *coordinate singularity* at r = 2m in the Painleve chart?

 

[Mentz114]

This is not correct. The horizon is a frame-independent, invariant feature of the geometry, and it's there regardless of what coordinate chart you use. Yes, the spatial sections in the Painleve chart are flat, but that doesn't mean an observer at r < 2m can send signals to r > 2m. The curvature of the spacetime that makes that impossible is all in the "time dimension" (so to speak) in the Painleve chart, but it's still there.

Edit: Maybe what you meant to say is that there is no *coordinate singularity* at r = 2m in the Painleve chart?

Yes. Thanks for the lecture, anyway.

 

[yuiop]

Yes, the equations would be nice. Plots (and even better animated plots) are extremely useful to get a quick overview of what an equation 'does'. In this day and age we have wonderful tools to visualize information and demonstrating something with a plot is an excellent means.

OK, here is how the equations to plot the paths in the https://www.physicsforums.com/showpost.php?p=2949294&postcount=79" were obtained.

The GP coordinates are given by Wikpedia as:

dt_{GP} = dt\, +(1-2m/r)^{-1} \sqrt{2m/r}\, dr

dr_{GP} = dr

Where dt and dr are the familiar Schwarzschild coordinates.

Now we know that the equation for a falling particle with apogee at infinity in Schwarzschild coordinates is dr/dt = -(1-2m/r)^{-1} (2m/r)^{-1/2} and we can substitute this equation into the definition of the GP time coordinate to elliminte dt and obtain:

dt_{GP} = - \sqrt{ \frac{r}{2m}}\, dr

(This turns out to be the same as the velocity measured by a local stationary Schwarzschild observer at r). Integrating the above gives the equation for the path of the falling particle in GP coordinates:

t_{GP} = -\frac{2r}{3}\sqrt{\frac{r}{2m}} +C

where C is a constant of integration.

Substitution of the GP time coordinate into the radial Schwarzschild metric gives the GP metric:

dtau^2 = (1-2m/r) dt_{GP}^2\, - 2\sqrt{2m/r}\, dr\, dt_{GP} \, - dr^2

Setting dtau = 0 gives the null path of a photon and solving the resulting quadratic gives the differential equation:

dr/dt_{GP} = (\pm 1)\, - \sqrt{2m/r}

where the sign is determined by whether the photon is ingoing or outgoing. For an ingoing photon the speed at the EH is -2c and the outgoing photon is zero.

Integrating gives the equations for the null paths in GP coordinates:

t_{GP} = r(2\sqrt{2m/r} \, \pm 1) - 4m\, \text{artanh}\left(1/\sqrt{2m/r}\right)\, \pm 2m \ln(r-2m) \, + C

or alternatively for the outgoing photon:

t_{GP} = r(2\sqrt{2m/r} \, +1) \, + 2m \ln\left((r-2m)\frac{1-\sqrt{2m/r}}{1+\sqrt{2m/r}} \right) \, + C

and for the ingoing photon:

t_{GP} = r(2\sqrt{2m/r} \, -1)\, - 2m \ln\left((r-2m)\frac{1+\sqrt{2m/r}}{1-\sqrt{2m/r}} \right)\, + C

The alternative form allows the null paths to be plotted across the event horizon without problems.

 

[JDoolin]

There is no horizon at r=2m in the Painleve chart.
The metric is

\begin{align*}<br /> \left[ \begin{array}{cccc}<br /> \frac{2\,M}{r}-1 &amp; -\sqrt{\frac{2M}{r}} &amp; 0 &amp; 0\\<br /> -\sqrt{\frac{2M}{r}} &amp; 1 &amp; 0 &amp; 0\\<br /> 0 &amp; 0 &amp; {r}^{2} &amp; 0\\<br /> 0 &amp; 0 &amp; 0 &amp; {r}^{2}\,{sin\left( \theta\right) }^{2} \end{array} \right]<br /> \end{align*}<br />
Note the flat spatial sections.

An observer at rest wrt to the 'rain', will see tidal tensor with T_{rr}=2m/r^3,T_{\theta\theta}=T_{\phi\phi}=-m/r^3

So the proper time of a particle in this region could be measured by:

<br /> ds^2=<br /> (dr^2<br /> -dt^2<br /> + r^2 d\theta ^2<br /> +r^2 \sin ^2 \theta d\phi ^2)<br /> +(\frac{ 2 M}{r}dt^2 <br /> -2 \sqrt{\frac{2 M}{r}} dr dt)​

This is the same as flat space except for the two terms at the end. Is this Painleve chart the same as the Schwarzschild metric?

This is not correct. The horizon is a frame-independent, invariant feature of the geometry, and it's there regardless of what coordinate chart you use. Yes, the spatial sections in the Painleve chart are flat, but that doesn't mean an observer at r < 2m can send signals to r > 2m. The curvature of the spacetime that makes that impossible is all in the "time dimension" (so to speak) in the Painleve chart, but it's still there.

Edit: Maybe what you meant to say is that there is no *coordinate singularity* at r = 2m in the Painleve chart?

What makes a heavy mass into a black hole is that it's own physical radius is smaller than its own horizon, right?

 

[Passionflower]

What makes a heavy mass into a black hole is that it's own physical radius is smaller than its own horizon, right?

I think a little more accurately stated:

An object becomes (or is already) a black hole if the ratio between the area it occupies and the area that represents its mass is smaller than 4. As soon as this happens the object's occupied area will shrink to zero.

E.g.:

<br /> {A_{occupied} \over A_{mass} } &lt; 4<br />

You notice that mass by itself is not in indication of whether something is a black hole or not, it is only the ratio that matters.

In general relativity mass is represented by a physical area.

Because spacetime is curved when we have mass it is no longer a trivial matter to derive a radius from those areas.

 

[JDoolin]

I live on a rocket that is under constant acceleration.

The rocket has many floors. My floor is labeled x=9.18 \times 10^{ 15} m, and on my floor, the gravity is g=c^2/x.

If I climb up, the gravity gets smaller. If I look up, the clocks above me are ticking faster.
If I climb down, the gravity gets greater. If I look down, the clocks below me are ticking slower.

If I drop something out the window, it falls down, and approaches a point c²/g below, but it will never reach there. The clocks down at that level (x=0) are not ticking at all and nothing can fall past them. If the rocket extended down that far, the gravity there would approach infinity.

I still need to determine the speed of the clocks as a function of either g or x. Then answer the more ambiguous question, is the speed of time determined by gravitational potential?

 

[granpa]

does this help?
http://math.ucr.edu/home/baez/physics/Relativity/SR/rocket.html

http://en.wikipedia.org/wiki/Rapidity

 

[JDoolin]

I still need to determine the speed of the clocks as a function of either g or x. Then answer the more ambiguous question, is the speed of time determined by gravitational potential?

An approximation follows:

We adopt a standard unit of time being the time it takes for an object to fall 1 meter. The following can only be used where x>>1, because when x is near or less than 1, the acceleration is not constant.

<br /> \begin{matrix}<br /> <br /> \Delta x = \frac{1}{2}g \Delta t^2 <br /> \\ \Delta t = \sqrt{\frac{2 \Delta x}{g}}= \sqrt{\frac{2}{g}}=\sqrt{\frac{2 x}{c^2}}<br /> \\ \frac{\Delta t(x)}{\Delta t(x_0)}=\sqrt{\frac{x}{x_0}}<br /> <br /> \end{matrix}<br />​

One interesting aspect of this is that the speed of time approaches infinity as x \to \infty. So as an ambiguous answer to my ambiguous question, the infinite speed of time would mean there is no natural zero for a corresponding gravitational potential.

 

[Passionflower]

If I drop something out the window, it falls down, and approaches a point c²/g below, but it will never reach there.

As soon as you drop something out of the window it is no longer in the accelerating frame you are describing but instead it is free falling and it keeps free falling forever.

The clocks down at that level (x=0) are not ticking at all and nothing can fall past them.

Close to this region clocks run slower wrt clocks higher up but locally clocks just run as normal. Free falling objects would pass by without hindrance.

I still need to determine the speed of the clocks as a function of either g or x. Then answer the more ambiguous question, is the speed of time determined by gravitational potential?

If I am not mistaken the relationship between proper time and coordinate time for a given acceleration is:

<br /> \tau={c\, \over \alpha} {\it arcsinh} \left( {\frac {\alpha t}{c}} \right)<br />

While the relationship between acceleration and position is:

<br /> \alpha={\frac {{c}^{2}}{x}}<br />