dekoi
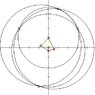
How does one find the most probable central location of something/someone when four points of their earlier location have been recorded and drafted? For example, if one is given points A, B, D, and C, how would they find the central location? This method must use cyclic quadrilaterals, and four circles which are each circumscribed by a different variation of three points.
````````````````A
B````````````````````````````C
`````````D
Perhaps the cyclic quadrilateral created by all the circumscribed circles' centers narrows down the location to inside the quadrilateral? Therefore, if one created a cyclic quad which touches all four origins, would the location be inside that cyclic quad? Maybe after drawing this cyclic quadrilateral which touches all four centers of the circles, one would connect opposite vertices, and the poitn at which both lines intersect, is the exact location.
However, that would not be using the cyclic quadrilateral created by the original points, A, B, C, and D.
````````````````A
B````````````````````````````C
`````````D
Perhaps the cyclic quadrilateral created by all the circumscribed circles' centers narrows down the location to inside the quadrilateral? Therefore, if one created a cyclic quad which touches all four origins, would the location be inside that cyclic quad? Maybe after drawing this cyclic quadrilateral which touches all four centers of the circles, one would connect opposite vertices, and the poitn at which both lines intersect, is the exact location.
However, that would not be using the cyclic quadrilateral created by the original points, A, B, C, and D.
Last edited by a moderator: