Qube
Gold Member
- 461
- 1
Represent the below vector relationship geometrically, illustrating two different ways of adding vectors.
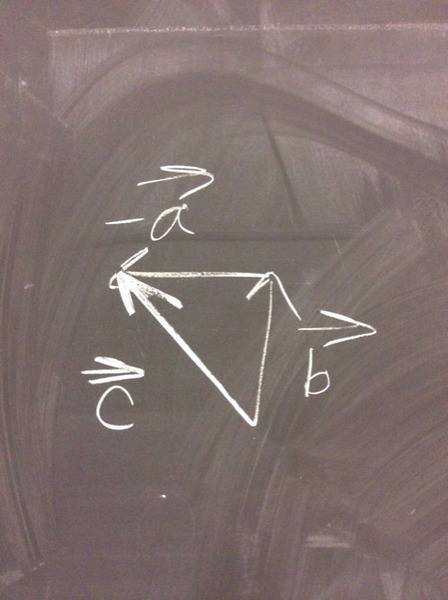
Vector a - vector b = vector c.
I know the above relationship can also be expressed as:
Vector a + (-vector b) = vector c.
In other words, we flip the direction of vector b and add as usual.
Attached are two pictures of me adding two *arbitrary* vectors a and b (vectors a and b change in the two attached photos).
In the first picture, I use the parallelogram rule. In the second picture, I use another method to add the arbitrary vectors a and b.
Did I add the two vectors together correctly?
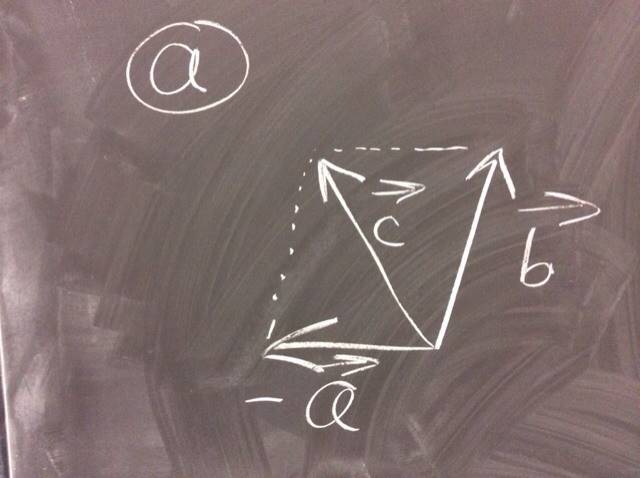
Vector a - vector b = vector c.
I know the above relationship can also be expressed as:
Vector a + (-vector b) = vector c.
In other words, we flip the direction of vector b and add as usual.
Attached are two pictures of me adding two *arbitrary* vectors a and b (vectors a and b change in the two attached photos).
In the first picture, I use the parallelogram rule. In the second picture, I use another method to add the arbitrary vectors a and b.
Did I add the two vectors together correctly?