Getting structure data from a partition function?

[maajdl]

Hello,

From wikipedia, this is the partition function for a "classical continuous system":

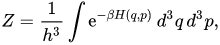
This is the pillar of classical statistical physics, but it can be seen as a mere kind of "mathematical transform" .
It can be used even without thinking to statistics or temperature.
If we focus only on the potential energy part of this integral, then

H = V(q)

is a function of q and the "positions of all other particles" of the system.

I question myself:
Would the full knowledge of Z(β) contain the full information about the "other particles".
And therefore, could the knowledge of Z(β) be traced back (inverted) to the positions of the atoms?

I hope this question doesn't look too fancyful.
I find it interresting because it would cast geometrical data in a 1-variable function Z(β) !

Thanks for your suggestions!

Michel

 

[Martin Scholtz]

Certainly no. Partition function is not a mathematical transformation (like Fourier) which has an inverse. It's more like averaging with weight given by the Hamiltonian. If you know the average, you cannot reconstruct the numbers that were averaged.

Moreover, partition function doesn't describe one particular configuration of the system. It is averaging through a domain in the phase space. Consider for example an ensemble of identical particles that have momenta but otherwise do not interact. Then the Hamiltonian has only kinetic part

$H = \sum\limits_i \frac{p_i^2}{2\, m}$

Then integral over dq gives just a trivial constant. Partition function does not serve to reconstruct details about microscopic quantities, only macroscopic ones.