BrainMan
- 279
- 2
Homework Statement
Two identical shuffleboard disks, one orange and the other yellow, are involved in a perfectly elastic glancing collision. The yellow disk is initially at rest and is struck by the orange disk moving with a speed of 4 m/s. After the collision, the orange disk moves along a direction that makes an angle of 30 degrees with its initial direction of motion and the velocity of the yellow disk is perpendicular to that of the orange disk (after the collision). Determine the final speed of each disk.
Homework Equations
The conservation of momentum
The Attempt at a Solution
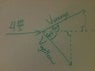
I knew that the initial momentum must be 4 because it is mv. I made both the masses to be one since they are equal to each other to make things simple. Then I tried to find each disks portion of the momentum through trigonometry. At first I treated each of the final velocities paths as the hypotenuses and the value of 4 as one of the sides but I got the wrong answer (see attached image). I eventually found the right answer by messing around with sin and cosine but I still can't visualize the triangles.