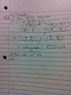fastXattack
- 3
- 0
Homework Statement
Show that the operation of taking the gradient of a function has the given property. Assume that u and v are differentiable functions of x and y and that a, b are constants.
Homework Equations
Δ = gradient vector
1) Δ(u/v) = vΔu - uΔv / v^2
2) Δu^n = nu^(n-1)Δu
The Attempt at a Solution
I tried taking the partial derivative of (u/v) and separating the terms but I didn't get the ending result.
For 2, I don't even know where to begin because it is an exponent.