Gravitational field Strength Inside the Earth

[Yh Hoo]

Since the Gravitational Attractive Force is given by, F_g=(Gm_1 m_2)/r^2

Let m_1be the minor mass of a small body (e.g. human) let m_2 be the massive mass of a huge spherically symmetric body (e.g. Earth)
Let r be the distance between the centre of the m_1 and m_2

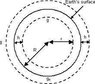
Generally, The Gravitational field strength experienced by the minor mass, m_1 would be = ((Gm_2)/r^2 ) N〖kg〗^(-1). This equation shows that the relationship between the distance,r and the gravitational field strength is actually an inverse square law. Now if we could drill a hole into the earth, the gravitational field strength decreases proportionally to the distance,r.
This effect is shown by the equation,
Gravitational field strength inside the earth=(G(4/3 πr^3⦁ρ_E )/r^2 ) N〖kg〗^(-1)
=( G(4/3 πr^1⦁ρ_E ) N〖kg〗^(-1)
## So what I concern is when this equation is used to show the relationship of direct proportion between the gravitational field strength and the distance between the core of the Earth to the object with mass m1(let it be r), it implies that we could directly assume that that object is now situated on the surface of the Earth but with a decreased volume and mass. Meaning we now just consider mass of the Earth partially, or we assume that the Earth shrink into a sphere with the same centre but a decreased radius. What about the rest of the mass of the Earth that is originally present ?? I tink there is another way of proving the directly proportional relation between the distance,r and the gravitational field strength. Can you please show it to me? Thanks a lot!

 

[Doc Al]

What about the rest of the mass of the Earth that is originally present ??

Look up Newton's Shell theorems. One of them shows that the gravitational field is zero anywhere inside a spherically symmetric shell of mass. Thus at any distance from the center D, only the part of the Earth where r < D will contribute to the gravitational field at that point.

(Of course we make the usual simplifying assumption of a spherically symmetric earth.)

 

[andrien]

there is no necessity of spherical shape.even if it is ellipsoid then it also holds here is an example from electrostatics which has an analogue in gravitation also.