Gravitational potential energy of a cylinder to a particle

[Gian Lukmana]

Hi everyone I'm kinda new here, your support will really be appreciated ! :D

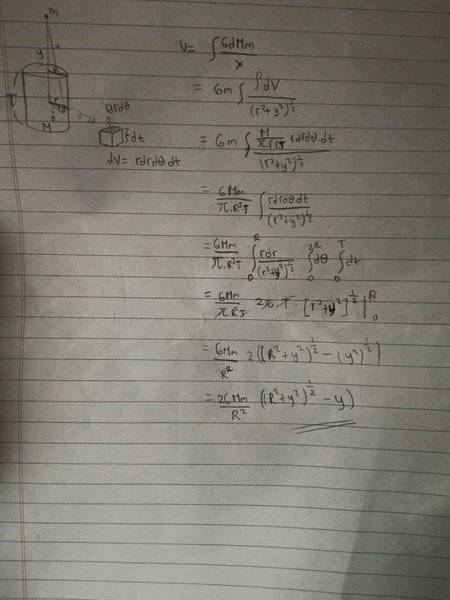
1. Homework Statement
Let's say the cylinder has radius R, and height T.

Homework Equations

U = ∫GmdM/x

The Attempt at a Solution

My attempt is shown in the picture, I took a tiny element of the cylinder with vertical distance y, and horizontal distance r from the particle, then I used integral. am I doing this right ? I think there's something odd with the "y" there. Should I range the y until the upper surface of the cylinder only?

 

[phinds]

Why would you need calculus for this? The volume of a cylinder can be looked up so if you have the density of the material, you can get the mass of the cylinder and the center of mass is trivially easy to get so if you have the mass of the particle, just plug everything into the gravity formula. Am I missing something about what you are trying to do?

 

[gneill]

Why would you need calculus for this? The volume of a cylinder can be looked up so if you have the density of the material, you can get the mass of the cylinder and the center of mass is trivially easy to get so if you have the mass of the particle, just plug everything into the gravity formula. Am I missing something about what you are trying to do?

The gravitational force due to a cylinder is not the same as that due to a sphere or point mass of the same mass. Geometry matters.

One approach would be to begin by finding the force exerted by a thin disk at a given distance, then treat the cylinder as a stack of such disks of thickness dy.

 

[Gian Lukmana]

Yeah, I heard that we can't treat other shapes as a sphere, so we can't just blindly use the normal formula. To confirm, does this mean y should be the distance of the particle and the upper surface of the cylinder ?

 

[gneill]

Yeah, I heard that we can't treat other shapes as a sphere, so we can't just blindly use the normal formula. To confirm, does this mean y should be the distance of the particle and the upper surface of the cylinder ?

I think it's up to you to specify your coordinate system and significant measurements, but it would probably make sense to characterize the setup by specifying distance of the test mass from the near end of the cylinder.

 

[Gian Lukmana]

alright, got it now, thank you so much !

 

[phinds]

The gravitational force due to a cylinder is not the same as that due to a sphere or point mass of the same mass. Geometry matters.

OOPS. Guess I didn't think that one through.