roshan2004
- 140
- 0
Homework Statement
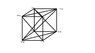
What is the gravitational potential energy of a system of 8 masses of 10 kg each placed at the corners of a cube of length 0.25 meter apart.
Homework Equations
U=-G*m1*m2/r
The Attempt at a Solution
I have actually taken one particle pair at a time and sum all of their potential energy, but the answer is not quite right.