Gravitational Time Dilation: A Thought Experiment

[Hurkyl]

And that was exactly the point that I brought up several postings ago.

In general relativity one cannot locally determine if one is in a gravitational field if this field is flat.

What do you mean by "gravitational field"? I know that I was assuming that you meant a force field, like the electic field, or the magnetic field, or the Newtonian gravitational field.

 

[nakurusil]

Instead think for instance of the inside of a hollow shell.
Do you think there is a gravitational field in the middle?

no

And if no, how would you explain the time dilation there (relative to someone far away removed from this shell).

Because there is gravitational time dilation between the "far away removed" and the surface of the shell. The calculations are elementary, didn't you know that? Try googling Pound-Rebka.

 

[RandallB]

Huh? That doesn't make it a preferred frame. That simply makes it the frame in which I chose to analyze the problem. It's basic coordinate geometry: if you want to solve a problem, you can impose a choice of coordiantes, express everything in terms of those coordinates, and algebraically work out the solution.

I don’t disagree with that, just the way you’ve analyze the problem incompletely. Impose instead a choice of coordinates that is moving at 0.5c along our flight path. At some instant after t = 0 the speed of the rocket, clocks, and string between the clocks will be in that reference frame and speed. Using the string example and your approach looking back from that frame you would find that the string must be shorter in length and therefore must necessarily have broken before the trip even started! Using my approach and seeing the distance between the attachment points as also shorter, you do expected it to break or have slack at one or the other observation point. Note also that the simultaneous start at t=0 for the two points (x=0) and (x=+rocket length) is no longer simultaneous from this new frame.
Likewise if you change your choice of coordinates to one where (x=0) is used for the front clock and the back clock is placed at (x=-rocket length) you will get inconsistent results, because your graph and your approach, as most, does not take simultaneity into account. And I see no reason to “favor” anyone of these reference frame choices.

Remember the Lorentz metric was designed with an aether in mind, SR does use the same metric, but it also requires dealing with the idea that simultaneity cannot be known with certainty from, or be based on, anyone frame.

 

[MeJennifer]

Because there is gravitational time dilation between the "far away removed" and the surface of the shell.

Well I am not talking about the surface of the shell but the inside of the shell.
How can you explain you have gravitational time dilation if you claim there is no gravitational field inside the shell?

Again, local curvature is no prerequisite for the presence of a gravitational field.

 

[Chris Hillman]

Bell redux

With due respect, I would at this point side with the Cern theoretic group in concluding that the string would not break.

This is doubly wrong. First, according to str, in Bell's thought experiment the string would break. This is easily confirmed by a simple computation, and also easily understood if you are familiar with the geometry of the Rindler congruence (note that the point is the Bell congruence is distinct from the Rindler congruence).

Second, if you read what Bell wrote again, you should see that this does not imply that all physicists currently at CERN currently believe that the string would not break.

But, as Bell points out, those who first reach this conclusion frequently change their mind after further consideration.

Because as a simple computation shows, etc., etc.

The expansion tensor is a standard quantity in (semi)-Riemannian geometry which is designed to automatically answer all such questions, and analyzing the Bell and Rindler congruences is a good way to get used to computing with frame fields and kinematic quantities like expansion.

I probably won't say very much in this thread if it devolves into arguing over how to do standard computations correctly (e.g. of the expansion tensor associated with some congruence).

 

[Chris Hillman]

Well sure your formula here is nice but your description of "constant" is wrong. The gravitational field here is only constant in the x & y directions (zero), not z.

Right, but Hurkyl did say "oriented along z", so while he could have written a bit less ambiguously, I think he appreciates this point.

 

[nakurusil]

Well I am not talking about the surface of the shell but the inside of the shell.
How can you explain you have gravitational time dilation if you claim there is no gravitational field inside the shell?

Again, local curvature is no prerequisite for the presence of a gravitational field.

You need to re-read what you asked. Just because the gravitational potential is null inside the shell, it doesn't mean that there is no time dilation for an observer placed inside the shell wrt a "far away source" placed outside the shell. The time dilation is exactly determined by the difference in graviational potential between the surface and the position of the "far away" source, ok?

 

[Chris Hillman]

"Lorentz metric designed with aether in mind"?

Remember the Lorentz metric was designed with an aether in mind

I squawk: the Minkowski metric we all know and love was introduced by Minkowski, but not with "an aether in mind". The notion of Lorentzian manifolds as used in physics was probably first concieved by researchers like Einstein and Nordstrom not long thereafter. If you trace back the mathematics, of course one can say that semi-Riemannian metrics appeared much earlier, e.g. in Cayley-Klein geometries, but these innovations had nothing directly to do with physics at all, much less an aether.

 

[nakurusil]

While this is a very interesting field I was not talking about this one.

Instead think for instance of the inside of a hollow shell.
Do you think there is a gravitational field in the middle?
And if no, how would you explain the time dilation there (relative to someone far away removed from this shell).

Here is exactly what you asked.

 

[MeJennifer]

You need to re-read what you asked. Just because the gravitational potential is null inside the shell, it doesn't mean that there is no time dilation for an observer placed inside the shell wrt a "far away source" placed outside the shell.

I am aware of the fact that there is a gravitational time dilation between the inside of the shell and a far away source.

The time dilation is exactly determined by the difference in graviational potential between the surface and the position of the "far away" source, ok?

I am not talking about the surface, I am talking about the inside of the shell. Anyway,... how come you say that inside the shell is no gravitational field?

In one sentence you say that the gravitational potential inside the shell is null and in another sentence you imply there is a difference in gravitational potential.
Doesn´t add up to me, does it to you?

Somewhow there seems to be a disconnect between what I think and what you think I think.

 

[Chris Hillman]

Would it help calm things down at all if I said that even professional physicists tend to get confused by the problem of physically interpreting the Lense-Thirring frame-dragging phenomenon? That there are various good reasons for preferring, in this context or that, one of a set of mutually inconsistent analogies between gtr and other classical field theories?

 

[nakurusil]

I

I am not talking about the surface, I am talking about the inside of the shell. Anyway,... how come you say that inside the shell is no gravitational field?

I said gravitational potential, not field. Do you know the difference?
The difference in gravitational potential is what causes the redshift.

In one sentence you say that the gravitational potential inside the shell is null and in another sentence you imply there is a difference in gravitational potential.
Doesn´t add up to me, does it to you?

Can you read? I said that the observed time dilation is due to the potential difference between the surface and the far away source.. So, if you live inside an empty shell and you observe a source up in the sky, you will see its frequency gravitationally shifted.
Your distance from the center of your sphere d<R has no influence on the amount of the shift, the altitude of the source h above the ground is all that counts.

Somewhow there seems to be a disconnect between what I think and what you think I think.

No question. As a third reminder, this is what you asked:

Do you think there is a gravitational field in the middle?
And if no, how would you explain the time dilation there (relative to someone far away removed from this shell).

And this is precisely what I answered.

 

[MeJennifer]

Ok, well then, let's agree to disagree.

 

[Hurkyl]

I don’t disagree with that, just the way you’ve analyze the problem incompletely.

Point at an actual mistake. I've worked the problem, and got results. If you think the result is wrong, that means I've made a mistake in my work. Show me that mistake.


You're switching to the string problem now, and not the two-clocks-on-one-rocket problem? Are we considering a version wher the rockets eventually stop accelerating, or one where they accelerate indefinitely? I'm going to assume indefinitely.

I can't really make heads or tails of your post. Too many things are simply nonsensical.

Let F0 denote the reference frame in which the rockets are initally at rest.

Impose instead a choice of coordinates that is moving at 0.5c along our flight path.

What does that mean? How can a coordinate chart be "along a flight path", let alone "moving along a flight path"?

I'm going to assume you intend for there to be a relative velocity of 0.5c between F0 and F1.

I would have guessed that you intended for the origin to lie along the path of one of the rockets, but that contradicts what you say next.

At some instant after t = 0 the speed of the rocket, clocks, and string between the clocks will be in that reference frame and speed.

I assume you mean t=0 as measured by F1. The rocket, clocks, and string are always in F1. Did you mean when they are at rest relative to F1?

You speak of some "instant" -- you seem to be assuming that, somewhere, both rockets, the string, and clocks (what clocks? There aren't any clocks in the string problem) are simultaneously at rest, as measred by F1.

That doesn't happen. Why would you think that it does?

(When I work the two-clocks-on-one-rocket problem, I never assumed that the two clocks are ever simultaneously at rest in any frame -- that is a fact I can prove as I work through the problem)

Using the string example and your approach looking back from that frame you would find that the string must be shorter in length

What does it mean to "look back from F1"?

Of course the string was shorter in the past -- that's what we've been trying to tell you: the string can't break in the future unless it was shorter in the past than it was in the future.

and therefore must necessarily have broken before the trip even started!

And this is exactly the opposite of what you just said!

Using my approach and seeing the distance between the attachment points as also shorter, you do expected it to break or have slack at one or the other observation point.

How do I see that? You have neither computed anything, nor suggested how you might have computed something.

Note also that the simultaneous start at t=0 for the two points (x=0) and (x=+rocket length) is no longer simultaneous from this new frame.

Of course. For exactly the same reason, in F1, the two rockets never have the same velocity simultaneously. In particular, they can never be simultaneously at rest. (as measured by F1)

Likewise if you change your choice of coordinates to one where (x=0) is used for the front clock and the back clock is placed at (x=-rocket length) you will get inconsistent results, because your graph and your approach, as most, does not take simultaneity into account. And I see no reason to “favor” anyone of these reference frame choices.

Show me the actual mistake. Point to something and demonstrate that it's mathematically in error.

The problem looks exactly the same in any reference frame. Lorentz transforms are symmetries of Minkowski space -- switching between different inertial frames when studying SR is no different than, for example, rotating a drawing when doing Euclidean geometry.

However, the two-clocks-on-one-rocket has an additional interesting (but aphysical) feature. Drawing the space-time diagram requires one to break the symmetry (since we're drawing the picture in Euclidean space), but the rocket problem is neat beacuse it looks exactly the same no matter how you draw it. (That is, if you use the related problem where the rocket has been accelerating for all times future and past)

To put it a different way, if you went back to my post and everywhere swapped "red" and "green", my analysis is still correct.


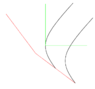
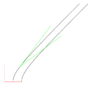
Aha! I have a drawing of the string problem. I didn't know where it would be reasonable to draw the string, so I just drew the rockets.

The red frame is the frame in which the rockets are initially at rest. The green frame is some other frame -- it's not precisely 0.5c: I picked a velocity in which it was convenient to program.

The origin of the green frame occurs where the leftmost rocket happens to be at rest in that frame. (plus or minus a pixel or two)

The black lines are the two rockets.


For fun, I've drawn the exact same picture twice. They represent exactly the same problem -- I just chose two different methods of drawing them in Euclidean space.

(I've gotten the drawing slightly off -- but it looks qualitatively the same as the true picture. I can fix it if you really disbelieve)

 

[Chris Hillman]

Point at an actual mistake. I've worked the problem, and got results. If you think the result is wrong, that means I've made a mistake in my work. Show me that mistake.

Uh oh, Bell's "paradox" may be claiming its latest victims! (That is, I quit WP last year because the rules then more or less required me and others to waste endless time arguing with someone who didn't accept standard computations of standard quantities. So I am sympathetic to Hurkyl's frustration here.)

RandallB, I haven't read the posts in question in any detail, in part because I figure I've enormously overpaid my dues in this topic, but I just wanted to suggest that you and Hurkyl might be talking about different things, so the alleged disagreement might be more apparent than real.

In particular, note that there are multiple distinct operationally significant definitions of "distance in the large" which Bell or Rindler observers can use, and also, of course, the Bell and Rindler congruences are significantly different (this is in fact Bell's point). But I think I'll leave it to others to sort out the details of this alleged disagreement.

Oh, and about the issue I like to call "will the real gravitational field please stand up?", this is not easy to explain, much less resolve, in a short space of time, in fact several thoughtful papers in the past few years have focused on this issue. As is so often the case in our subject, it turns out there are various mutually inconsistent analogies which are valuable for different purposes, so it is probably wisest to resist the temptation to claim that my challenge could ever result in a unique quantity stepping forward from the crowd.

 

[RandallB]

Originally Posted by RandallB
Well sure your formula here is nice but your description of "constant" is wrong. The gravitational field here is only constant in the x & y directions (zero), not z.

Right, but Hurkyl did say "oriented along z", so while he could have written a bit less ambiguously, I think he appreciates this point.

What does that have to do with not using a "constant" value in that direction but claiming it is constant. Gravity on Earth does not remain constant with hieght z?

Also, we call them Lorentzian for the formulas that started from his efforts to explain failing to detect the aether due to physical things changing length in the direction they move through it. Long before using them with Minkowski.

not with "an aether in mind".

 

[RandallB]

Point at an actual mistake. I've worked the problem, and got results. If you think the result is wrong, that means I've made a mistake in my work. Show me that mistake.

You're switching to the string problem now, and not the two-clocks-on-one-rocket problem? Are we considering a version wher the rockets eventually stop accelerating, or one where they accelerate indefinitely? I'm going to assume indefinitely.

I can't really make heads or tails of your post. Too many things are simply nonsensical.

Let F0 denote the reference frame in which the rockets are initially at rest.

?? You haven’t recognized the string with the front attached to a clock in one rocket the back attached to a clock on a following rocket is essentially the same problem as your two clocks in one rocket problem? If you don’t get that no wonder I cannot make heads or tails of your complaints. Neither problem calls for stopping, and I didn’t ask for them to stop, just a revelation of an instant in the future when the two were in the frame that moves at 0.5c with respect to your F0 frame.

As to “point at an actual mistake”, here’s the best I can do for you.
Instead of having the two rockets take off at the same time and acceleration from F0; take the point you’re making your measurements from in F0 and accelerate that in opposite direction you were going to send the rocket(s). When you work this problem and graphs your results from that point you will still get the same results of clocks running at different rates or the string breaking (or getting slack). Even though in this example the rocket(s) haven’t even moved, but do appear to be accelerating from the relative measure of your observation point. The clocks, or string, in fact could not do that as they didn’t even move.

IMO the reason that such effects can look correct, come from the same errors that are often made in thinking “The Twins” don’t age differently, that was my first mistake I held with conviction for awhile when starting out in understanding relativity. That taught me to very careful about simultaneity issues. The approaches I’ve seen here do not do that IMO. If you do not agree with that, then there is little chance we will ever agree with each other on this paradox, so we should just end this.

 

[Chris Hillman]

I can't tell from a quick glance if either RandallB or Hurkyl believes the other is arguing that a string stretched between two observers in the Bell congruence would not break (in fact it would), much less whether either is in fact making that claim.

Still trying to spread oil on the troubled waters: it is quite possible you two don't actually disagree about anything, just that some misunderstanding arose, probably from being insufficient precision in describing a thought experiment.

 

[RandallB]

I can't tell from a quick glance if either RandallB or Hurkyl believes the other is arguing that a string stretched between two observers in the Bell congruence would not break (in fact it would),

That just says you need more than a quick glance.
Hurkle is actually talking about a single rocket with two clocks; I see that as including the problem of the string. Provided the whole rocket accelerates uniformly; so that we do not have to deal with "jerk" (acceleration of acceleration) compression oscillations going up and down the material the rocket is made of.
I assume you agree with him that two clocks on one rocket would run at different rates of time; along with somehow defining gravity on Earth as constant as altitude changes and that you both think the string breaks.
As I just said in my prior post if you use an accelerating observation point and frame give you the same results even though the rocket or string doesn’t actually move.
With just a quick glance, you are only contributing or voting your preconceived notions, not putting oil on the water.

As I’ve said, if you guys do not think a more rigorous treatment of simultaneity is called for on these issues we will never agree. If so I’m willing to leave this and simply say that there is a chance that Hurkle is as right as I am, and I might be as wrong as Hurkle is.

 

[Hurkyl]

?? You haven’t recognized the string with the front attached to a clock in one rocket the back attached to a clock on a following rocket is essentially the same problem as your two clocks in one rocket problem?

Of course I don't: they aren't the same problem. They aren't even analogous problems.

In this picture, I've drawn three problems.

Problem 1:
On the red coordinates, I've drawn the one-rocket-with-two-clocks problem. The two black lines are the worldlines of the head and tail. The gray area is the worldsheet traced out by the rocket.

Problem 2:
On the green coordinates, I've drawn the two-rockets-and-string problem. The two black lines are the worldlines of the two rockets (assumed to be point-particles). The blue area is the worldsheet tracet out by the string.


Of course, if you so desired, you could combine the two problems into one grand problem:
Problem 3:
On the blue coordinates, I've drawn the two-rockets-and-string problem where I've treated the rockets as extended objects, rather than point particles.

just a revelation of an instant in the future when the two were in the frame that moves at 0.5c with respect to your F0 frame.

Why do you think such a thing exists in the two-rockets-and-string problem?

take the point you’re making your measurements from in F0

I don't follow. F0 is a frame. Frames assign coordinates to every events. My measurements are the coordinates assigned by F0.

and accelerate that in opposite direction you were going to send the rocket(s).

Although I'm not sure just what you mean, it sounds like you are telling me to measure things with respect to some noninertial "frame" F2. It's not clear to me exactly what noninertial frame: I think you're telling me that the t-axis should trace out the path of a hypothetical uniformly accelerated particle that started at rest at the origin of F0... presumably so that F2's time coordinate coincides with the proper time experienced by the hypothetical particle. But I don't know how you want to assign coordinates to the rest of Minkowski space.

That taught me to very careful about simultaneity issues. The approaches I’ve seen here do not do that IMO. If you do not agree with that, then there is little chance we will ever agree with each other on this paradox, so we should just end this.

Care is good. But I don't understand what you find lacking in my treatment, nor do I see rigor in yours.

Look at this picture again. My biggest "Eureka!" moment for SR is essentially that you don't have to Lorentz transform into the green coordinates in order to figure out the length of the rocket at t=0[/color]. Length, as measured by the green frame, is nothing more than the proper length of a segment of a line of simultaneity[/color]. That segment is indicated in the middle of the picture. I know how to compute that proper length using the red coordinates, so I never have to bother with a Lorentz transform.

(as always, green text indicates things relative to the green coordinate chart)

This led me to realize that SR is a geometric theory, and it eventually sunk into my head that only Lorentz invariant quantities matter -- everything else is just an artifact of how you're analyzing the problem.

I worry that your approach is fundamentally misguided -- you seem to be extremely insistant that one chooses their coordinate frame properly, and keeps switching between frames to analyze different parts of the problem. But a choice of coordinate chart is completely aphysical: it has absolutely no bearing on the problem. If you get right answers by doing it, then good -- but I fear you are completely missing what's happening in SR!

 

[MeJennifer]

I am getting interested in accelerating clocks.

Let me get this absolutely right:

In flat space-time, two completely identical ideal clocks sepearated by a distance l accelerate with a constant proper acceleration a for an identical proper time interval t.
After completion, each clock sends a digitally encoded signal of its value to a remote observer.
After the observer receives both encoded signals he decodes them and concludes that the sent clock readings are not identical?

Is that what is claimed?

 

[RandallB]

My biggest "Eureka!" moment

Well maybe you need another one.
I note you did not draw the diagrams as seen from a single point on F0 from the view of accelerating that point (and its reference frame view of F0) in the opposite direction without moving the clocks or string at all.
Also the fact that you can fit the clocks and the string onto a single diagram as you did is proof enough that the two are related problems.

OH, but wait you did give three diagrams from the view of an accelerating point without the clocks or string moving at all.
The same three diagrams you gave for holding the observation point stationary. This must prove that string tied to fixed points will break spontaneously! I’ve put up a sting and am waiting for it to break, but no luck so far. Maybe it means that it won’t break unless some accelerating observer goes by and actually looks at the string and its attachment points! But that would mean the moon is not really there unless someone looks at it, and I don’t buy that view either.

As to the frame for speed 0.5c of course both clocks must eventually be in that frame, what are you thinking. The only question is at what point and time in that frame is clock A at a speed of zero in relation to that frame, it can only be a single point and time and what time is on clock A as well. Likewise for clock B, it cannot be the same point in the 0.5c frame. So now how do the numbers compare; is there a difference in time in that frame for those two points? What is the distance between the two points in that frame? And how does the time on clock A, compare to clock B?
It takes detail like this to understand the twin’s paradox, and you simply haven’t gone though enough detail to come to a convincing final conclusion on this problem.
You are just repeating the same pattern and answer as before, which IMO and a moving F0 doesn’t work.

 

[Jorrie]

I am getting interested in accelerating clocks.

Let me get this absolutely right:

In flat space-time, two completely identical ideal clocks separated by a distance l accelerate with a constant proper acceleration a for an identical proper time interval t.
After completion, each clock sends a digitally encoded signal of its value to a remote observer.
After the observer receives both encoded signals he decodes them and concludes that the sent clock readings are not identical?

Is that what is claimed?

I have also puzzled about this fact and came to the following conclusion, right or wrong (to be determined ).

What you described is equivalent to two static clocks sitting at different gravitational potentials in a hypothetical uniform gravitation field. They suffer identical gravitational accelerations (due to the uniform field), yet they suffer different gravitational time dilations (or gravitational redshift as measured by a distant static observer), due to their different potentials.

Herein lurks the problem: their identical proper-time intervals (t, that you specified) per definition means that they send the exact same time stamp to the remote observer - yet they did not send it simultaneously... simultaneous in whose reference frame?

Hope it helps, otherwise ignore!

Jorrie

 

[pervect]

I am getting interested in accelerating clocks.

Let me get this absolutely right:

In flat space-time, two completely identical ideal clocks sepearated by a distance l accelerate with a constant proper acceleration a for an identical proper time interval t.
After completion, each clock sends a digitally encoded signal of its value to a remote observer.
After the observer receives both encoded signals he decodes them and concludes that the sent clock readings are not identical?

Is that what is claimed?

Clarify something, please. Is the constant proper acceleration a identical for both clocks? Or do both clocks maintain a constant distance L? The two conditions are, as I have mentioned once or twice :-), different and incompatible.

 

[RandallB]

equivalent to two static clocks sitting at different gravitational potentials in a hypothetical uniform gravitation field. They suffer identical gravitational accelerations

If they are at different gravitational potentials they cannot produce identical gravitational accelerations. You need to construct a constant gravitation field as noted earlier (that means not a round mass like Earth).

 

[MeJennifer]

Ok, let me try to make it as unambigious as possible:

In flat space-time, two completely identical ideal clocks separated by an initial distance l accelerate with a constant proper acceleration a for a proper time interval t.
After completion, each clock sends a digitally encoded signal of its value to a remote observer.
After the observer receives both encoded signals, which he may or may not receive at the same time, he decodes them and concludes that the sent clock readings are not identical?

Is that what is claimed?
And is this the situation of the Bell spaceship paradox?

 

[Jorrie]

Uniform gravitational field

If they are at different gravitational potentials they cannot produce identical gravitational accelerations. You need to construct a constant gravitation field as noted earlier (that means not a round mass like Earth).

OK, maybe the term uniform gravitational field was a bad choice of words. Let's replace uniform gravitational field with uniform gravitational potential gradient in a specific direction. Now gravitational potential linearly change in that direction, while gravitational acceleration remains constant.

This, IMO, represents the situation of linear acceleration where the "g-meters' on the two clocks, line astern, read the same acceleration, while the gravitational redshift differs. The front clock gains time on the rear clock.

Jorrie

 

[pervect]

Ok, let me try to make it as unambigious as possible:

In flat space-time, two completely identical ideal clocks separated by an initial distance l accelerate with a constant proper acceleration a for a proper time interval t.
After completion, each clock sends a digitally encoded signal of its value to a remote observer.
After the observer receives both encoded signals, which he may or may not receive at the same time, he decodes them and concludes that the sent clock readings are not identical?

Is that what is claimed?
And is this the situation of the Bell spaceship paradox?

Yes, to the BSP paradox question, this is one common form of the BSP. But onto the original question.

Let's make the comparison process a bit more specific. It's rather vague right now.

An observer, exactly midway between the two spaceships, receives their time readings. Does he receive the same value?

This is more specific, but still not specific enough. While we've specified the position of the observer (he's midway between the two clocks) we haven't yet specified his velocity. This is a key omission, as differently moving observers will answer the question differently.

If the observer is at rest relative to the initial velocity of the clocks, before they started accelerating, he will find that he receives the same encoded signal values.

IF the observer is at rest relative to the _final_ velocity of the clocks, after they are through accelerating, he will not receive the same encoded signal values.

A space-time diagram would be helpful in understanding these results, you might also want to look at

http://en.wikipedia.org/wiki/Relativity_of_simultaneity

 

[MeJennifer]

Let's make the comparison process a bit more specific. It's rather vague right now.

Ok, I apologize for being vague, so let´s pin this down a bit more, I am sure you agree that being vague or beating around the bush does not serve anything.

So,

In flat space-time, two completely identical ideal clocks separated by an initial distance l accelerate with a constant proper acceleration a for a proper time interval t. After this time interval each clock stops counting but leaving the final time on their displays.

An observer fetches both clocks and compares the time as displayed on their displays.

Are the readings identical or not?

 

[Jorrie]

... IF the observer is at rest relative to the _final_ velocity of the clocks, after they are through accelerating, he will not receive the same encoded signal values.

Hi Pervect, as you usually say: Huh?

OK, a misunderstanding. MeJennifer specified (paraphrased) "after an identical proper-time t, the two clocks send encoded signals..."

The time stamps on these signals are the same, by definition. As I tried to point out in post #83, they were just not sent out simultaneously in the frame of the observer.

Jorrie