Gross Pitaevskii one dimensional solution

[Yoris21]

Hey guys, new to the forum here! I'm having this excercise where I have to prove that the solution of Gross Pitaevskii in one dimension, is equal to: φ(x)=Ctanh(x/L) for a>0 and φ(x)=C'tanh(x/L). The differential equation goes like this:

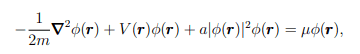
Any thoughts on what approximations do I have to use?

 

[Fred Wright]

It's very annoying when people post homework problems and show no attempt at the solution. It shows that you are either lazy or your course work is beyond your abilities and it's an insult to others who show effort. It's against the PF rules for me to help you if you show no effort but I will give you some hints because I don't have the patience to hold your hand through this problem. Hopefully, in your next post you will show some effort.

First, the Gross-Pitaevskii equation has no closed form solution when $V(\vec r) \ne 0$.

Second, with $V(\vec r) = 0$ you have a second order, homogeneous, non-linear differential equation (very hard to solve). Why don't you use $\phi (x) = C \tanh (\frac{x}{L})$ as a trial solution?

Third, you need boundary conditions. Remember that you are dealing with a soliton. I suggest,
$$
\lim_{x \rightarrow +\infty} \phi (x)=0
$$
$$
\lim_{x \rightarrow +\infty} \frac{d\phi (x)}{dx}=0
$$
With these boundary you can evaluate $C$ and $L$. I'll leave it to you to justify the use of these boundary conditions.

 

[Yoris21]

Hi, thanks for your response. As I said in my first sentence, I am new to the forum here, so I am not yet quite familiar with the forum rules. I accept that this excercise may be beyond my abilities, however, you should also be more polite to people that you don't know, either you have the upper hand on them, or not. You have no idea what effort anyone makes for their work, therefore you should not conclude in such allegations.