lolly
- 1
- 0
Hello!
I have written the code in Maple for Heat equation with Neumann B.C. Could anyone check it? I will be very grateful!
Heat equation: diff(u(x,t),t)=diff(u(x,t),x,x);
Initial condition: U(x,0)=2*x;
Boundary conditions: Ux(0,t)=0; Ux(L,t)=0;
I use centered difference approximation for the Neumann conditions. For my case:
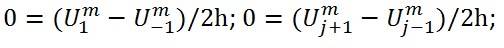
The code:

I really do not know about my mistakes. I know how to solve it with Dirichle B.C. But I do not know how to write the code in Maple for Neumann B.C.
Thank You!
I have written the code in Maple for Heat equation with Neumann B.C. Could anyone check it? I will be very grateful!
Heat equation: diff(u(x,t),t)=diff(u(x,t),x,x);
Initial condition: U(x,0)=2*x;
Boundary conditions: Ux(0,t)=0; Ux(L,t)=0;
I use centered difference approximation for the Neumann conditions. For my case:
The code:
I really do not know about my mistakes. I know how to solve it with Dirichle B.C. But I do not know how to write the code in Maple for Neumann B.C.
Thank You!