Nusselt
- 2
- 0
Moved from a technical forum, so homework template missing
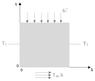
Summary:: Determine the temperature distribution in a bar (very long– 2D) with rectangular cross section, in steady state, with imposed flux at one face, convection at the opposing face (Tinf, h), and imposed temperature (T1) at the two remaining walls.
I am trying to find the analytical solution to the following problem :
Determine the temperature distribution in a bar (very long– 2D) with rectangular cross section, in steady state, with imposed flux at one face, convection at the opposing face (Tinf, h), and imposed temperature (T1) at the two remaining walls.
I have the differential equation and four boundary conditions , however I can't find the temperature distribution even using the supeposition method ( trying to find the solution with one of the walls adiabatic and the other transferring energy by convection and then finding the solution for one of the walls adiabatic and the other with imposed flux).
Has anyone came across a problem like this?
I am trying to find the analytical solution to the following problem :
Determine the temperature distribution in a bar (very long– 2D) with rectangular cross section, in steady state, with imposed flux at one face, convection at the opposing face (Tinf, h), and imposed temperature (T1) at the two remaining walls.
I have the differential equation and four boundary conditions , however I can't find the temperature distribution even using the supeposition method ( trying to find the solution with one of the walls adiabatic and the other transferring energy by convection and then finding the solution for one of the walls adiabatic and the other with imposed flux).
Has anyone came across a problem like this?
Attachments
Last edited by a moderator: