Ampere
- 44
- 0
Homework Statement
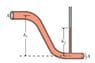
An upper tube of cross sectional area A, atmospheric pressure, and height h1 is connected to a lower tube with cross sectional area A/2 (and height 0). A fluid of uniform density rho flows through the system, with velocity v measured in the upper tube. A small open tube branches up off the lower one, with a column of fluid of height h2 inside it. Find h2.
(See attached diagram.)
Homework Equations
Bernoulli's equation,
P1 + pgh1 +1/2*pv12 = constant
Continuity equation,
A1v1 = A2v2
The Attempt at a Solution
Applying Bernoulli's equation between the top of fluid of height h2 and the left endpoint of the system, I got:
(point 1 = left endpoint, point 2 = top of the column with height h2)
P1 = atmospheric
P2 = atmospheric
KE1 = 1/2*rho*v2
KE2 = 0
PE1 = rho*g*h1
PE2 = rho*g*h2
Therefore h2 = h1 + v2/(2g). Is this right? I would think that a faster moving fluid pushes h2 up even higher (with h2 = h1 when v=0).
The continuity equation tells us that the speed of the fluid inside the smaller tube is 2v. But does this even matter?
Attachments
Last edited: