Height Required for Rollercoaster to Remain on the Track

[B3NR4Y]

Homework Statement

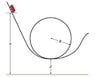
A roller-coaster car initially at a position on the track a height h above the ground begins a downward run on a long, steeply sloping track and then goes into a circular loop-the-loop of radius R whose bottom is a distance, d, above the ground in the figure. Ignore friction. At what minimum value of the starting height h above the ground must the car begin its journey if it is to remain on the track at the top of the loop?

Homework Equations

a=v²/r
Energy is conserved

The Attempt at a Solution

The first parts of the problem had me calculate the speed at the bottom of the loop, a quarter of the way up the loop, the normal force at the bottom and the normal force at a quarter of the way up. I got the following answers:
v_{bottom} = \sqrt{2gh-2gd} I got this by energy conservation. F^{N}_{bottom} = m\frac{2gh-2gd}{R}+mg I got this by circular motion, where I know the acceleration is given by a=v²/r, which would be the sum of the forces in the y direction, I just solved for the normal force. v_{\frac{1}{4}} = \sqrt{2gh-2g(d+R)} I got this by geometry and energy conservation. The normal force at that position is F^{N}_{\frac{1}{4}} = m\frac{2gh-2g(d+R)}{R}. Using these I calculated the Normal force at the top of the loop and the velocity at the top of the loop. I got v_{top} = \sqrt{2gh-2g(2R+d)}. The Normal force is F^{N}_{top} = mg - \frac{2gh-2g(2R+d)}{R}. I'm not sure where to start. For it to stick to the top, it would have to have enough energy to make it to the top of the loop, so I tried an answer of 2R+d, but that's wrong. I just need a hint, really.

 

[Simon Bridge]

To have enough energy to make it to the top of the loop, it needs only for h=2R+d.
However, that would make it stop at the top of the loop, and fall down.

What do you need for it to stick and keep going in a circle?
Hint:
At the top of the loop - what are the forces?
You can get an expression for the initial potential energy of the car - what is the potential energy at the top of the loop?
What is the kinetic energy?

 

[B3NR4Y]

At the top of the loop the forces are the centripetal force and the force of gravity, I think.
At the top of the loop, it's potential energy would be mg(2R+d), and the kinetic energy would be 1/2 (m) (2gh-2g(R+d)

For it to not fall down, it would have to have enough speed to maintain a circular motion, I suppose, but I am not sure where to start figuring that out. It confuses me that the normal force and the force of gravity act in the same direction, and all the forces on the object seem to be down yet it doesn't fall down. I guessed that the cart would have to be going around the circle at the top point faster than it is falling for it to stay in touch with the tracks, but that doesn't help me solve the problem. I'm confused the more I think of it.

 

[Orodruin]

What force is necessary to keep the cart in circular motion when it reaches the top? What force is generally required to keep an object in circular motion?

 

[Ray Vickson]

At the top of the loop the forces are the centripetal force and the force of gravity, I think.
At the top of the loop, it's potential energy would be mg(2R+d), and the kinetic energy would be 1/2 (m) (2gh-2g(R+d)

For it to not fall down, it would have to have enough speed to maintain a circular motion, I suppose, but I am not sure where to start figuring that out. It confuses me that the normal force and the force of gravity act in the same direction, and all the forces on the object seem to be down yet it doesn't fall down. I guessed that the cart would have to be going around the circle at the top point faster than it is falling for it to stay in touch with the tracks, but that doesn't help me solve the problem. I'm confused the more I think of it.

At the top both forces point down, so the direction of acceleration is downward. If it has some horizontal velocity at that time, it will start to curve down, just enough to follow the downward-curving track.

 

[B3NR4Y]

The force needed for it to stay in circular motion is the centripetal force, so F^C = mv^2/R

F_g=F^C
mg = mv^2/R, I know v already
so I solved for it and v=\sqrt{Rg} and since I know v to be \sqrt{2gh-2g(2R+d)} I can put it into that equation and get 2gh-2g(2R+d) = Rg. Then I solved this equation for h, I got \frac{R+2(2R+d)}{2} = h

Am I doing this right or did I make a stupid mistake?

 

[Orodruin]

Looks reasonable.

 

[mfb]

The answer is correct. I would write it as d+2R+R/2 or d+5/2 R, however.