Michael_0039
- 59
- 7
- Homework Statement
- The position of a material point in a Cartesian coordinate system 0XYZ given from the equation r=( 3sin(t) , 3cos(t) , 4t ), t : time. Describe in a few words the motion and find the route's length (arc length) from t=5 to t=10. Calculate the accelerattion vector and the radius of curvature at every point on the track.
- Relevant Equations
- r = ( 3sin(t) , 3cos(t) , 4t )
I have tried to solve it and I would like a confirmation, correction or if something else is suggested... :)

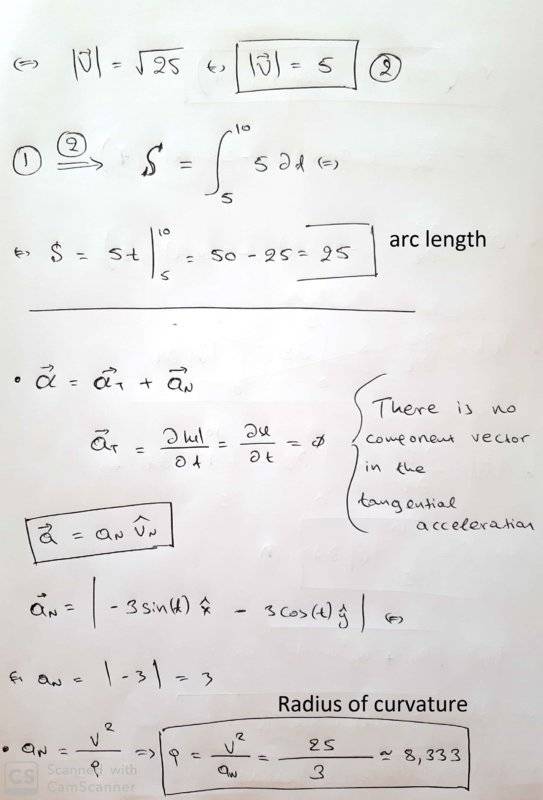
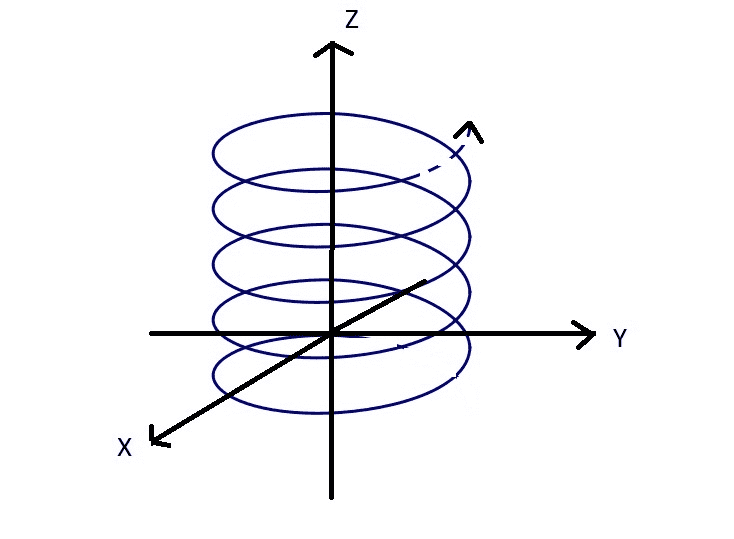
Helicoidal movement
Helicoidal movement