Science4ver
- 35
- 0
Homework Statement
Hi guys,
I have a problem here.
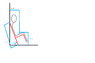
A man is sitting on a chair leaning at 60 degrees against a friction-less wall. The height of the chair is 1.20 meters and the distance between the man's center of mass and the wall is 0.5 meters. The distance between the guy's knees and the floor while the chair is leaning is 0.9 meters.
The weight of man + chair is 80 kg. Note the guy is assumed to be sitting still and will be moving while leaning against the wall.
1) Calculate the force between man+chair and the wall and calculate the force between man+chair and the floor.
Homework Equations
Newton 2. law
The Attempt at a Solution
In order to calculate these force I use the equilibium equations.
Thusly \sum F_y = m_{c+m} \cdot g \cdot sin(60) \cdot 1.2 - F_{wall}=0
and \sum F_x = m_{c+m} \cdot g \cdot cos(60) \cdot 0.5 - F_{floor}=0
and I on the right track here guys?
Attachments
Last edited: