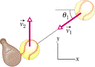noname1
- 131
- 0
A 0.300 kg baseball just before and after it collides with a bat. Just before, the ball has a velocity v1 of magnitude 12.0 m/s and angle θ1 = 35°. Just after, it is traveling directly upward with velocity v2 of magnitude 10.0 m/s. The duration of the collision is 1.5 ms.
(a) What is the magnitude of the impulse on the ball from the bat?
I tried solving a by
pi = (.3)(12)(cos215i+sin215j) = -2.95i + 2.06j
pf = (.3)(12)j = 3.6j
i = pf - pi = 3j - (-2.95i - 2.06j) = 2.95i +5.66j
mag = sqrt(2.95²+5.66²) = 6.38
what am i doing wrong?
(a) What is the magnitude of the impulse on the ball from the bat?
I tried solving a by
pi = (.3)(12)(cos215i+sin215j) = -2.95i + 2.06j
pf = (.3)(12)j = 3.6j
i = pf - pi = 3j - (-2.95i - 2.06j) = 2.95i +5.66j
mag = sqrt(2.95²+5.66²) = 6.38
what am i doing wrong?