nchin
- 172
- 0
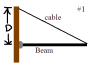
#1 a uniform beam of weight 500 N and length 3.0 m is suspended horizontally. On the left is hinged to the wall; on the right it is supported by a cable bolted to the wall at distance D above the beam. The least tension that will snap the cable is 1200N. What value of D corresponds to that tension?
TLcos(θ) - mg L/2 = 0
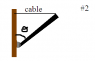
#2 a uniform beam of length 12.0 m is supported by a horizontal cable and a hinge at angle θ = 50° with the vertical. The tension in the cable is 400 N. Find the gravitational force on the beam in unit vector notation and the force on the beam from the hinge in unit vector notation.
TLsin40° = W(L/2)sin50°
I am confused on when to use cos or sin. Can someone explain why cos was use in #1 and sin in #2? I attached some pics below.
TLcos(θ) - mg L/2 = 0
#2 a uniform beam of length 12.0 m is supported by a horizontal cable and a hinge at angle θ = 50° with the vertical. The tension in the cable is 400 N. Find the gravitational force on the beam in unit vector notation and the force on the beam from the hinge in unit vector notation.
TLsin40° = W(L/2)sin50°
I am confused on when to use cos or sin. Can someone explain why cos was use in #1 and sin in #2? I attached some pics below.