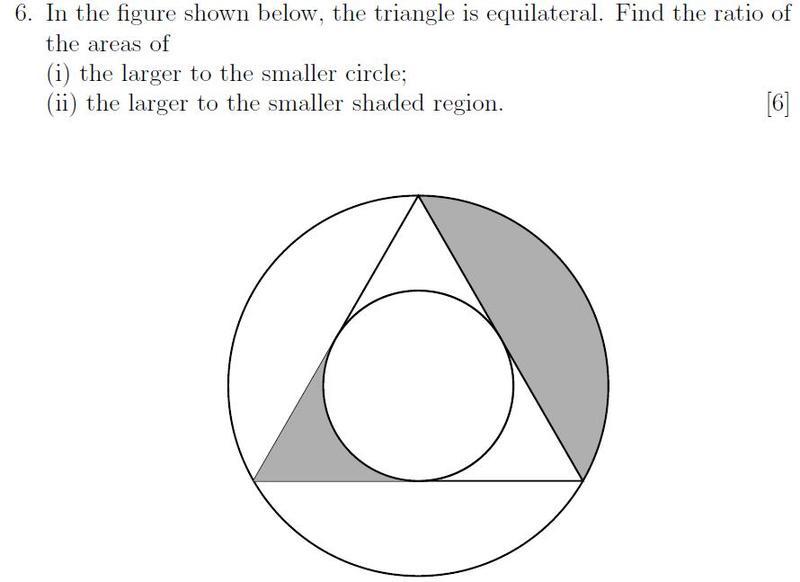
SUMMARY
The radius of the larger circle is not twice that of the smaller circle; rather, the ratio of their radii is 3:1. This conclusion is derived from geometric principles involving an equilateral triangle and the application of the Pythagorean theorem. Specifically, the radius of the larger circle is calculated as R = L/√3, while the radius of the smaller circle is R = (√3/6)L. The relationship between the sides of the triangle and the radii of the circles is crucial for understanding this geometric configuration.
PREREQUISITES
- Understanding of basic geometric principles, particularly involving circles and triangles.
- Familiarity with the Pythagorean theorem and its application in right triangles.
- Knowledge of trigonometric functions, specifically sine values for angles 30° and 60°.
- Ability to manipulate algebraic expressions to derive relationships between geometric elements.
NEXT STEPS
- Study the properties of equilateral triangles and their relationship to inscribed circles.
- Learn about the application of the Pythagorean theorem in various geometric contexts.
- Explore trigonometric ratios and their use in solving geometric problems.
- Investigate the derivation of circle properties from inscribed polygons.
USEFUL FOR
Mathematicians, geometry students, educators, and anyone interested in understanding the relationships between geometric shapes and their properties.