Help needed for a magnetism problem which is somewhat disturbing

[mooncrater]

Homework Statement

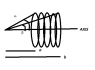
the problem is as: a very long straight solenoid has a cross section R and n turns per unit length . A direct current I flows through the solenoid . Suppose that x is the distance from the end of the solenoid , measured along its axis:
(a) the magnetic induction B on the axis as a function of x.
(b) the distance x' to the point on the axis at which the value of B differs by η=1% from that in the middle point of the solenoid.

Homework Equations

B=μnI[cosβ-cosω]/2
is what I use for the (a) part , by putting the value β and ω where β is angle made by the axis and the end part of the solenoid and ω is the angle made by the axis and starting part of the solenoid.
And n is the number of turns [per unit length.

The Attempt at a Solution

I am cool with the first part of the question. But the problem occurs with the second part.
I start with the second part as:
magnetic field at the centre of the solenoid = μnI[cos 0 - cos 180]/2=μnI
( What I think that for a long solenoid both the angles tend to 0 and 180 respectively for β and ω
)
1% deviation from this value is asked thus-
μnI -μnI/100=μnI[cosβ-cosω]/2
99μnI/100=μnI[b/rt.(b^2+x^2)+a/rt.(a^2+x^2)]
now what is x'-----not clear
is x' related to a and b (distance of that point from front and end respectively )----not clear

so that's it .
mooncrater

 

[BvU]

Strange that you are happy with a) and don't need R there. (does R have the dimension of length or of area ? usually we have R for radius, D for diameter and something like S for cross section area).

My hunch is you do need R and also the length of the solenoid in b).

To you x' is not clear, but for me as a reader, I can't make out what a and b are, either. Could you explain? And perhaps make a drawing ?

[Edit] Ah! distance to front and end. And rt means square root. Try the Go Advanced button; it has a √ symbol at the ready...

By the way, the μnI can be divided out to get a clearer perspective ... then the whole thing is just a simple gonio exercise.

 

[BvU]

Oh, and there is something wrong with the expressions for cosines. If you make a drawing, you'll see it. Hint: don't use a and b but use x' - L/2 and x' + L/2 . And be sure to maintain the - sign .

 

[BvU]

Oh 2: just to get an impression, check how much B has dropped already at the end of the coil: $\beta = \pi/2$, $\omega = \pi$, gives half the B at the center ! So our x' should be well within the coil!

 

[mooncrater]

oh 1: correction

Oh, and there is something wrong with the expressions for cosines. If you make a drawing, you'll see it. Hint: don't use a and b but use x' - L/2 and x' + L/2 . And be sure to maintain the - sign .

you are right i am mistaken in writing the distance version of the formula , I think the correct one is ;
B=μni[b/√(b²+R²)-a/√(a²+R²)]
where R is the radius of cross section of solenoid.

 

[BvU]

Apart from the factor of 1/2, yes.
The choice of coordinates suggested in the a) part of the exercise is somewhat awkward ("x is the distance to the end of the solenoid -- measured along its axis").
It is good to read you are comfortable with that part of the exercise.

1. What exactly is the answer you came up with ?
2. Does it match with my wild hunch in post #4, B = μnI/2 when x = 0 ?
3. And at what x is B = μnI ?

For part b) you now have two variables, a and b, where there is only one degree of freedom. Some way or other, you want to write one equation with one unknown.

Did you make a drawing ? If so, can you share it ?

 

[mooncrater]

the drawing is attached

 

[mooncrater]

see , the problem I am facing is that what is x' actually-
1) distance from the edge of the coil ?
2) distance from the centre of the coil?
i came up with the answer-
b/√(b²+R²)-a/√(a²+R²)=198/100
and now I am stucked with converting a and b into x' , and while thinking about it's solution one can also think about the length of the solenoid , but the only thing about the solenoid's length given is that it's LONG. so, it's clear we can't use it's length for deriving the result we want.

 

[BvU]

We will need the length of the solenoid. Call it L, remove b and use a + L instead, and continue.
Usually people take the center of the coil as coordinate system origin, but in the a) part of the exercise a clear choice was already made to make x = 0 when a = 0 (or b = 0). As you have already calculated in the a) part, B is μnI/2 there (please confirm) for an infinitely long coil. So not the 99% of μnI.

To answer b) properly, drop the infinite length and use L to get an expression for B(x'). Solve for B(x')= 0.99 B(L/2) (the latter is slightly less than μnI, which may or may not make a difference...).

Note that μnI can be divided out, leaving a simple goniometric equation.