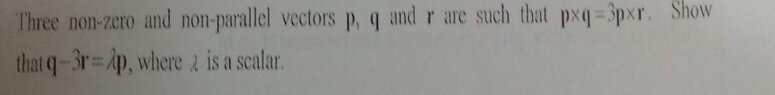- #1
Joe20
- 53
- 1
I have done up some of the steps. I got stuck and not sure how to continue. I am not sure if those steps are correct. Need help on that.
View attachment 7976
View attachment 7975
View attachment 7976
View attachment 7975
Attachments
Last edited by a moderator: