physicsismydaddy
- 1
- 0
Need some help on a practice physics problem.
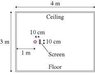
You need to place a mirror on the left wall, so that the reflected light from the bulb exactly fills the right wall.
ceiling
_________________________
| |
| |
3m | |
| 0 |
| |
| |
_________________________
4m
- the light bulb is 1m away from the left wall, it looks like it is centered.
a. what is the proper height of the mirror?
b. how far below the ceiling should the edge of the mirror be?
c. a 10cm tall screen to the right of the bulb from illuminating the right wall directly, what is the height of the screen's shadow on the right wall?
how I've approached the problem thus far: I started by stating that the angle that the top right corner makes with the mirror's top should be theta reflective and the other angle to the source from the mirror would be theta incidence due to the law of reflection. I'm lost as to where to go from here.
You need to place a mirror on the left wall, so that the reflected light from the bulb exactly fills the right wall.
ceiling
_________________________
| |
| |
3m | |
| 0 |
| |
| |
_________________________
4m
- the light bulb is 1m away from the left wall, it looks like it is centered.
a. what is the proper height of the mirror?
b. how far below the ceiling should the edge of the mirror be?
c. a 10cm tall screen to the right of the bulb from illuminating the right wall directly, what is the height of the screen's shadow on the right wall?
how I've approached the problem thus far: I started by stating that the angle that the top right corner makes with the mirror's top should be theta reflective and the other angle to the source from the mirror would be theta incidence due to the law of reflection. I'm lost as to where to go from here.