- #1
sullyjared
- 6
- 0
[SOLVED] help! where can i find mass?
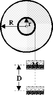
A spool of thin wire (with inner radius R=0.50m outer radius R=o.65m, and a moment of inertia I_cm=0.8957 kg*m^2) pivots on a shaft. The wire is pulled down by a mass M=1.5 kg. After falling a distance D=0.51m, starting from rest, the mass has a speed of v=64.5 cm/s. Calculate the energy lost to friction during that time.
KE=.5Iw^2
KE=.5mv^2
v=rw
I=.5M(r^2+R^2)
I have made two attempted solutions for this problem. The first was simple. I neglected the spool all together. Then I solved for the potential energy of the mass pulling down and the kinetic energy of this mass, and found the difference... that didn't work.
My second attempt was to calculate the kinetic energy of the spool with KE=.5Iw^2 and compare it to the Kinetic energy of the mass pulling down but to solve for the spools kinetic energy i need the moment of inertia about the axis of rotation, which means i need the mass of the spool, which i don't have... any suggestions?
Homework Statement
A spool of thin wire (with inner radius R=0.50m outer radius R=o.65m, and a moment of inertia I_cm=0.8957 kg*m^2) pivots on a shaft. The wire is pulled down by a mass M=1.5 kg. After falling a distance D=0.51m, starting from rest, the mass has a speed of v=64.5 cm/s. Calculate the energy lost to friction during that time.
Homework Equations
KE=.5Iw^2
KE=.5mv^2
v=rw
I=.5M(r^2+R^2)
The Attempt at a Solution
I have made two attempted solutions for this problem. The first was simple. I neglected the spool all together. Then I solved for the potential energy of the mass pulling down and the kinetic energy of this mass, and found the difference... that didn't work.
My second attempt was to calculate the kinetic energy of the spool with KE=.5Iw^2 and compare it to the Kinetic energy of the mass pulling down but to solve for the spools kinetic energy i need the moment of inertia about the axis of rotation, which means i need the mass of the spool, which i don't have... any suggestions?
Attachments
Last edited: