fdajkffk
- 14
- 0
From my Math Textbook
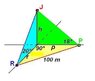
Suppose Romeo is serenading Juliet while she is on her balcony. Romeo is facing north and sees the balcony at an angle of elevation of 20 degrees. Paris is observing the situation and is facing west. Paris sees the balcony at an angle of elevation of 18 degrees. Romeo and Paris are 100m apart. Determine height of balcony above the ground.
How do I solve this question?
Attempt:
I was able to find the angles of the top two triangles but I do not know where to go from there. I do not have enough information to use cosine law or sine law in order to find the height of this balcony.
Suppose Romeo is serenading Juliet while she is on her balcony. Romeo is facing north and sees the balcony at an angle of elevation of 20 degrees. Paris is observing the situation and is facing west. Paris sees the balcony at an angle of elevation of 18 degrees. Romeo and Paris are 100m apart. Determine height of balcony above the ground.
How do I solve this question?
Attempt:
I was able to find the angles of the top two triangles but I do not know where to go from there. I do not have enough information to use cosine law or sine law in order to find the height of this balcony.