Nordcus
- 1
- 0
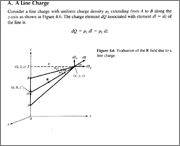
Hey guys, can someone please help me with this? In the case of the line charge (pictures 1 and 2), can someone please explain to me how he converted the vector R from cartesian coordinates to cylindrical coordinates without doing any calculation?
Also, on the case of the sphere (pictures 3 and 4), I didn't understand how he got the components cos(alpha) az and sin(alpha) ap of the vector ar.
Can someone please recommend me some material or book to study this subject about orthogonal basis of cylindrical and spherical coordinates?
Sorry for my bad english, and thank you very much.



Also, on the case of the sphere (pictures 3 and 4), I didn't understand how he got the components cos(alpha) az and sin(alpha) ap of the vector ar.
Can someone please recommend me some material or book to study this subject about orthogonal basis of cylindrical and spherical coordinates?
Sorry for my bad english, and thank you very much.