Help with Eulers relation in Fourier analysis

[Huumah]

Hi I'm doing Fourier analysis in my signals and system course and I'm looking at the solution to one basic problem but I'm having trouble understanding one step

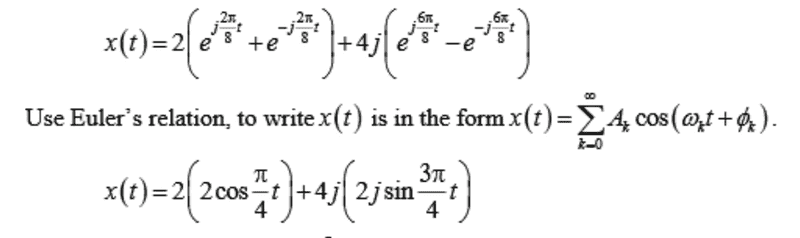
Can anyone explain to me why

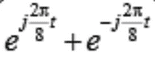
becomes

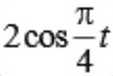
From Eulers formula: http://i.imgur.com/1LtTiKX.png

for example the Cosine in my problem. I thought the "twos" would cancel each other but instead becomes 4 and simular for the sine.

 

[CompuChip]

If
\cos z = \frac{e^{jz} + e^{-jz}}{2}
then multiply everything by 2 to get
2 \cos z = e^{jz} + e^{-jz}

Or you can use the identity
e^{jz} = \cos(z) + j \sin(z)
and also immediately get
e^{jz} + e^{-jz} = \cos(z) + j \sin(z) + \cos(z) - j \sin(z) = 2 \cos(z)