Discussion Overview
The discussion revolves around modeling the orbital dynamics of a celestial body in relation to a fixed mass, focusing on the trajectories that can result from different initial conditions. Participants explore the implications of gravitational forces on orbital paths, including potential spiraling behavior and the mathematical frameworks necessary for analysis, particularly in a calculus context.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
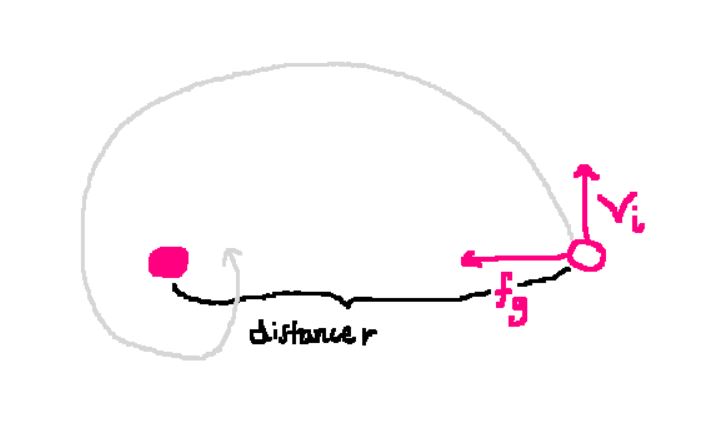
- William B expresses a desire to model a scenario where a celestial body spirals towards a larger mass, indicating a preference for a larger mass M and outlining the need for calculus in this task.
- One participant asserts that without an external force, the celestial body cannot spiral in, stating that only open (hyperbolic or parabolic) or closed (circular or elliptical) trajectories are possible based on the initial velocity relative to a specific threshold.
- Another participant reiterates the trajectory types and introduces the concept of effective potential energy, suggesting that the motion should be analyzed with respect to this equation.
- A question is posed regarding the background knowledge of participants, specifically if they have taken a Classical Mechanics course, implying that understanding may vary among participants.
- A detailed explanation of Keplerian orbital elements and their calculations is provided, including examples of Earth's orbit and a hyperbolic orbit, outlining the mathematical processes involved in determining position and velocity from these elements.
Areas of Agreement / Disagreement
Participants do not reach consensus on the possibility of spiraling trajectories, with some asserting that it is not feasible under the conditions described, while others explore the implications of effective potential energy. The discussion remains unresolved regarding the initial conditions and their effects on the trajectory types.
Contextual Notes
The discussion includes various assumptions about gravitational influences and the definitions of trajectory types. There are unresolved mathematical steps related to the calculations of orbital elements and their implications for motion.
Who May Find This Useful
This discussion may be of interest to students and enthusiasts of classical mechanics, orbital dynamics, and calculus, particularly those looking to understand the complexities of celestial motion and gravitational interactions.