SELFMADE
- 80
- 0
I need help understanding this notation, what does this mean?
Squared of 2-norm?
1. Homework Statement
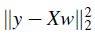
Thanks
Squared of 2-norm?
1. Homework Statement
Thanks