Henry gets into an elevator on the 50th floor

  • Thread starter p14r
  • Start date
  • Tags
    Elevator
In summary, Henry's mass is 91.84 kg and his maximum apparent weight within the elevator is 900.0N. On the graph, the maximum apparent weight occurs at the highest point and the minimum apparent weight occurs at the lowest point. The elevator's motion is causing these readings, with the normal apparent weight occurring when the elevator is at rest.
  • #1
p14r
4
0
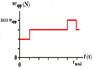
Henry gets into an elevator on the 50th floor of a building and it begins moving at t=0.00 s. His apparent weight is shown over the next 36.0s


What is Henry's mass if his maximum apparent weight within the elevator is 900.0N?

so shouldn't it just be:
w = mg
m = w/g
= 900/9.8
= 91.84 kg

but I keep getting the answer wrong.
 

Attachments

  • graph.jpg
    graph.jpg
    8.1 KB · Views: 416
Physics news on Phys.org
  • #2
Can you identify on your graph where the maximum apparent weight occurs? How about his minimum apparent weight?

attachment.php?attachmentid=62357&stc=1&d=1380638363.gif


What do you suppose is happening with the motion of the elevator to cause these readings? Where would you expect to see his normal apparent weight?
 

Attachments

  • Fig1.gif
    Fig1.gif
    7.9 KB · Views: 674

FAQ: Henry gets into an elevator on the 50th floor

1. How long will it take for Henry to reach the ground floor?

Without knowing the speed of the elevator, it is impossible to determine the exact time it will take for Henry to reach the ground floor. However, on average, elevators travel at a speed of 500 feet per minute. Therefore, assuming the elevator travels at this speed, it would take approximately 5 minutes for Henry to reach the ground floor from the 50th floor.

2. Is it safe for Henry to be in an elevator on the 50th floor?

Yes, it is safe for Henry to be in an elevator on the 50th floor. Elevators are designed and built to safely transport people from one floor to another. As long as the elevator is properly maintained and used correctly, there is no reason to believe that it is unsafe for Henry to be in it.

3. Can the elevator stop working while Henry is inside?

Yes, it is possible for the elevator to stop working while Henry is inside. However, elevators have multiple safety mechanisms in place to prevent this from happening. In the rare event that the elevator does malfunction, there is an emergency button or phone that Henry can use to call for help.

4. How many floors does the elevator have?

The number of floors in an elevator can vary depending on the building it is installed in. However, most elevators in commercial and residential buildings have a maximum of 60 floors. Therefore, it is safe to assume that the elevator in this scenario has 50 floors.

5. Can Henry control the elevator himself?

No, Henry cannot control the elevator himself. Elevators are operated by trained professionals who control the movement of the elevator using a control panel. However, in some elevators, there may be a "door open" or "door close" button that allows passengers to manually open or close the elevator doors.

Similar threads

Solving for weight and mass in kg in an elevator
Replies
2
Views
3K
Elevator Problem Apparent weight and distance traveled
Replies
1
Views
10K
Forces acting on a box-pulley system in an elevator?
Replies
33
Views
7K
Need help finding the acceleration for this question
Replies
9
Views
4K
How Does Elevator Physics Affect the Work Done by a Cable?
Replies
2
Views
2K
Finding Mass and Distance using apparent Weight
Replies
17
Views
19K
The elevator, the scale, and the wrong answer: Solving the Puzzle
Replies
7
Views
9K
Elevator Problem w/ app. Weight
Replies
2
Views
6K
Apparent weight loss 2nd Newtons Law elevator problem
Replies
4
Views
2K
Work Done by Elevator Cable in Sample Problem 7-6
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top