GeorgeWBush
- 6
- 0
This is my first post and is for an applied project (not for a class) but I thought this was the best place to ask for help.
Given a cylindar on its side, with volume V, length L, and Radius R, what is height (h) of liquid. I have fomula for volume as a function of radius, length, and height, but when I try to solve for h, things get difficult.
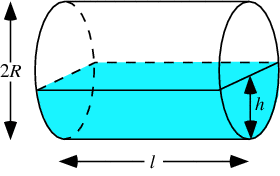
and
http://mathworld.wolfram.com/images/equations/CylindricalSegment/equation2.gif
1) divide both sides by L
2) square both sides
3) expand polynomials
4) get stuck, post this message
Homework Statement
Given a cylindar on its side, with volume V, length L, and Radius R, what is height (h) of liquid. I have fomula for volume as a function of radius, length, and height, but when I try to solve for h, things get difficult.
Homework Equations
and
http://mathworld.wolfram.com/images/equations/CylindricalSegment/equation2.gif
The Attempt at a Solution
1) divide both sides by L
2) square both sides
3) expand polynomials
4) get stuck, post this message
Last edited by a moderator: