Hole in a container and its distance from the bottom

[brunettegurl]

Homework Statement

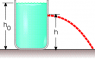
A hole is punched at a height h in the side of a container of height h₀ = 1.15 cm. The container is full of water, as shown in the figure below. If the water is to shoot as far as possible horizontally, how far from the bottom of the container should the hole be punched?

Homework Equations

P=\rhogh

The Attempt at a Solution

as this question deals with fluid mechanics i know we need to know the pressure and so on. we know that density of water is 1000kg/m³. and we have height of the whole container but i have no idea how to make the connection...pls. help

 

[kbaumen]

A general advice would be to express d (the distance) as a function of h (height of the hole) and find the maximum of this function.

You will need to apply some basic kinematics, i.e. find how max(d) relies to v, the velocity of the water stream pouring through the hole.

Btw, Bernoulli's principle will also be of some help.

 

[brunettegurl]

so i used the equation P1+ \rhogh+0.5*\rhoV²=P2+\rhogh+o.5*\rhoV²
and solved for v2 which is \sqrt{2g*(ho-h)}

i know i can use the equation x=V2*t solve for t and put it into the equation y=-0.5*g*t^2 and solve for h or y in this case but i have no idea what to put for my x value as it only says If the water is to shoot as far as possible horizontally, how far from the bottom of the container should the hole be punched?... pls. help

 

[brunettegurl]

so i got a message that i think was meant for the thread but don't see it here and this is what it said :: "Your solution for v2 looks good. In order to maximize the horizontal distance the water shoots, you'd have to maximize its horizontal exit exit speed from the container, v2, would you not? Looking at your equation, that occurs when h = ?"

I'm unsure of what they mean that i can determine height from just looking at the equation as well as the fact i don't know how to determine max distance the water hits on the ground

 

[brunettegurl]

nvm i realized my mistake yet again ..thank you for the help

 

[brunettegurl]

but i do have a question i realized that when it comes out of the spot it will have maximum distance coverage if it was halfway of the cylinder..is there another way to do the question??

 

[PhanthomJay]

but i do have a question i realized that when it comes out of the spot it will have maximum distance coverage if it was halfway of the cylinder..is there another way to do the question??

Sorry, I deleted my earlier post response that was not correct, but I guess I wasn't quick enough on the trigger. I am not sure how you arrived at the correct answer that the hole should be halfway down the tank for max range. I had to do it using calculus to find the max value of x (the horizontal distance) from the differentiation of the x =f(h) equation (as kbaumen has suggested) , such equation which can be derived from the kinematic equations you alluded to. Once you have x as a function of h, then set dx/dh = 0 and solve for the value of h =ho/2.