physics_31415
- 7
- 0
Homework Statement
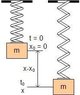
See attachment (titled "Statement.jpg")
Homework Equations
F = ma
F = -kx
U = K = (1/2)kx^2
I'm assuming there are more...
The Attempt at a Solution
My first attempt at this soultion was to use energy methods. The force applied for some time t0 will displace the block by some distance x. I then calculated the potential energy in the spring and used COE. However I eneded up with a useless result. It was something like (x-x0)^2 = (x-x0)^2.
Any hints you can give me will be GREATLY appreciated! I have also attached the free-body diagram that I came up with (titled "FBD.jpg"). Thank you in advance!