Hopf Fibration, torus with fibers, do it 2 ways?

[Spinnor]

The following is a projection of a set of fibers of a 3-sphere?

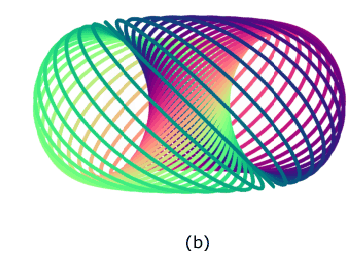
Consider the mirror image of the above,

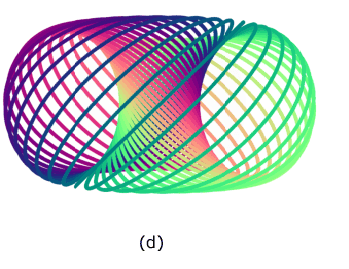
Can the 3-sphere be rotated so that (b) becomes (d)?

Is there an easy way to understand this?

Thank you.

 

[fresh_42]

Looks like a rotation around the y-axis by $\pi$.

 

[Spinnor]

Looks like a rotation around the y-axis by $\pi$.

That is a rotation of the 3-sphere around its y axis, 1 = x^2 +y^2 +z^2 +w^2 or of the y-axis of the image above? Are they the same?

Then one image should smoothly "morph" into the other?

Thanks.

 

[Spinnor]

If one imagines a physical torus with the above lines of (b) drawn on it and one rotates it in front of you "end over end" (b) does not change into (d)? But if we rotate a 3-sphere can the projection (b) "morph" into the projection (d)?

Thanks.

 

[fresh_42]

I have a very poor geometric phantasy. I even do not really understand its standard picture. That's why I approached it algebraically:
https://www.physicsforums.com/insights/journey-manifold-su2mathbbc-part/

 

[Spinnor]

very poor geometric phantasy

Could you put that in other words? Thanks.

 

[fresh_42]

imagination

 

[Spinnor]

imagination

You mathematical brute, you!

And if it not obvious, the above is a complement.

 

[Spinnor]

Maybe the answer is in this video below, the parts of the fibers closest to you seem to mostly go from "top left to bottom right". Just an observation not at all mathematical.

 

[Spinnor]

So I think I have an answer to my original question which was the title of this thread,

Hopf Fibration, torus with fibers, do it 2 ways?

I think that the answer to my question is yes and there are 2 fibrations that cannot be rotated into each other? To understand this requires only some simple assumptions about Hopf Fibrations which I think to be true.

Imagine a very large 3-sphere and the set of fibers of its fibration. Pick a point of this 3-sphere and consider a fiber that goes through this point. Now with the point and the fiber we can define a 2-sphere that goes through the point, is perpendicular to the fiber, and divides the 3-sphere in two equal halves? Our fiber actually goes through this 2-sphere at 2 antipodal points and is perpendicular at both points? Now surround this fiber with with a small torus of radius r such that the fiber is perfectly centered in the center of the torus. This torus is in fact the union of 2 inequivalent sets of fibers, typical fibers shown in yellow and blue of the projection of our torus below? Ignore the green and light blue lines below.

If we were in the 3-sphere we would not see the image above but see a "straight" fibered torus. Keep that picture in your head, what you would actually see because under a rotation of the 3-sphere what you see does not change, the 3-sphere and its fibrations rotate "rigidly"? The two fibrations are inequivalent and can not be rotated into one another?

Please point out where I may have made questionable assumptions.

Thanks.

Image captured from,

 

[Nickajeglin]

I think you are right. One thing you mentioned sticks out to me as a solid negation of morphing one to the other.

Imagine that you begin simultaneously rotating all the fibers as if to "morph" to the other configuration. As they become parallel to the axis of the torus, they will trace circumferences of the torus. For this to be possible, the fibers must be unlinked.

I think the concept of a "smooth morph" requires that the fibers are linked at all time. Since there is a point halfway through the transformation where it is impossible for the fibers to be linked, then it is also impossible for them to make a smooth transition from the left hand configuration to the right hand one.

I think this primitive mental proof relies on a particular definition of "continuous". My calculus is strong, but the different types of continuity and analysis type underpinnings are a little arcane for me. Hopefully a mathematician will drop by and hand out some wisdom on that

 

[WWGD]

I think you msy want to look inho the fundamental groups of the sphere. I understand the Hopf Fibration is a non-trivial element of them ( I believe in this case both groups are equal/isomorphic). Edit: It, the Hopf map, generates $\pi_3(S^2)= \mathbb Z$, so the Hopf map is the only non-homotopically -trivial ( class of ) map(s) from $S^3$ to $S^2$. I think @lavinia or @mathwonk may be able to verify this. It's been a while since I've seen this material.

 

[Spinnor]

Had some time to think about the above. It may help to graph some of the fibers that make up a cylinder that surrounds a single fiber,

The graph above is meant to represent a cylinder that surrounds a single fiber. On this graph are drawn four fibers. As this cylinder sits in 3-dimensional space we can give it an orientation, let out of the computer screen be the outside of the cylinder. Thus defined the solid lines represent fibers of left-handed helicity and the dashed lines represent right-handed fibers? Each fiber links the central fiber once? In three space dimensions shape of a curve defines it's helicity? Physical rotation of a helix does not change it's helicity? Rotation of a three-sphere does not change a fibers helicity? There exist two inequivalent fibrations of a three-sphere of different helicity?

I think the statements with question marks are true but would appreciate corrections.

 

[lavinia]

Maybe the answer is in this video below, the parts of the fibers closest to you seem to mostly go from "top left to bottom right". Just an observation not at all mathematical.

Love the rockin' torus.

Here is another nice graphic

https://samuelj.li/hopf-fibration/

 

[Spinnor]

There may be another proof lurking in the group of rotations in 4 dimensions, SO(4)? The Wiki page on rotations in 4-dimensional Euclidean space has an image and comment,

"A 4D Clifford torus stereographically projected into 3D looks like a torus, and a double rotation can be seen as in helical path on that torus. For a rotation whose two rotation angles have a rational ratio, the paths will eventually reconnect; while for an irrational ratio they will not. An isoclinic rotation will form a Villarceau circle on the torus, while a simple rotation will form a circle parallel or perpendicular to the central axis."

https://en.wikipedia.org/wiki/Rotations_in_4-dimensional_Euclidean_space#Double_rotations

There are two families of "double" rotation that give the "flow" above and also its mirror inverse?

Thanks.

​