SUMMARY
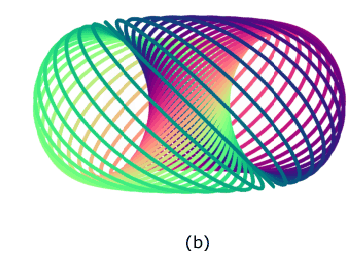
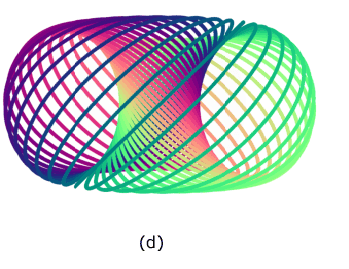
The discussion centers on the Hopf Fibration and the possibility of morphing two distinct projections of a 3-sphere's fibers. Participants conclude that a rotation around the y-axis does not allow for a smooth transition between the two configurations due to the linked nature of the fibers. The conversation highlights the importance of understanding the non-trivial elements of the Hopf map, particularly its role in generating the fundamental group of the sphere, specifically ##\pi_3(S^2)= \mathbb Z##. The participants agree that the two fibrations are inequivalent and cannot be transformed into one another through rotation.
PREREQUISITES
- Understanding of Hopf Fibration and its properties
- Familiarity with the concept of fibers in topology
- Knowledge of fundamental groups in algebraic topology
- Basic understanding of rotations in four-dimensional space
NEXT STEPS
- Study the properties of the Hopf map and its implications in topology
- Explore the concept of fiber bundles and their applications in mathematics
- Learn about the fundamental groups of spheres, particularly ##\pi_3(S^2)##
- Investigate rotations in four-dimensional Euclidean space and their geometric interpretations
USEFUL FOR
Mathematicians, topologists, and students interested in advanced concepts of fiber bundles and the geometric properties of higher-dimensional spaces.