- #1
rollcast
- 408
- 0
I've heard of curves being described as one dimensional but I don't understand how anything other than a straight line can be one dimensional as surely once the curve becomes, well, curved it is now in two dimensions?
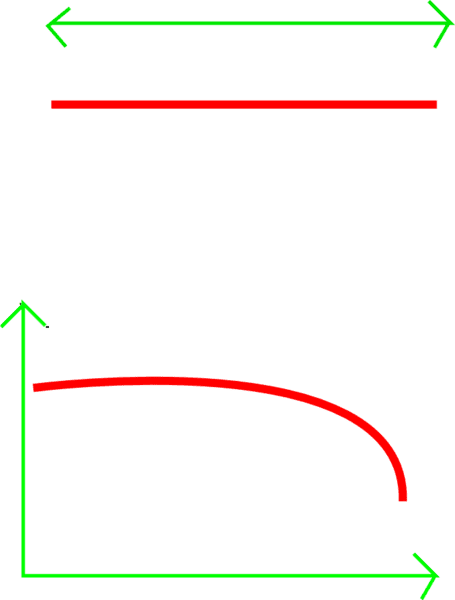
I have illustrated this in the above diagram with the curve and straight line shown in red and the dimensions in green.
Thanks
A.
I have illustrated this in the above diagram with the curve and straight line shown in red and the dimensions in green.
Thanks
A.