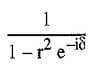How can complex numbers be expressed with a real denominator?

[patm95]

Homework Statement

Express (see attachment) with a real denominator

Homework Equations

Not sure if there is really relevant equations to use here.

The Attempt at a Solution

First I multiply the top and bottom by the exponential. That gives me e^ix/(e^ix-r^2). I think this is a good first step, but I am unsure where to go from here.

 

[Mentallic]

To make the denominator real (called rationalizing the denominator) you need to convert it into the form a+ib and then multiply by its complex conjugate a-ib. Can you turn it into that form first? It will be easier if you convert e^ix into its polar form expression.

 

[patm95]

If I convert the denominator as given in the problem I end up with: i r^2 sin(x)+r^2 (-cos(x))+1 I don't see how I can make a conjugate with 3 variables here? Am I missing something? I have went over this several times in attempt to make sure I hadn't made a mistake...

 

[vela]

I take it r and δ are real. If that's the case, it's a bit simpler to simply replace i with -i to form the conjugate of the denominator, rather than converting to rectangular form. Use the fact that $z+\bar{z} = 2 \textrm{Re}(z)$ to simplify the cross term.

 

[Pengwuino]

Whenever you have a problem of the form $$\frac{a}{b}$$ where 'a' and 'b' are in general, complex, you can immediately multiply top and bottom by the conjugate of b.

$$\frac{a}{b} \frac{b^*}{b^*}$$

and the result in the denominator is b*b = |b|, which is always real.

If $$r, \delta$$ are real, the only change when you conjugate is changing the sign on the i's.

 

[HallsofIvy]

You don't have to write the complex number as a+ bi. Just multiply both numerator and denominator by the complex conjugate, $1- r^2e^{i\delta}$. You get
$$\frac{1- r^2e^{i\delta}}{1- r^2(e^{i\delta}+ e^{-i\delta})+ r^4}$$
$$= \frac{1- r^2e^{i\delta}}{1+ r^4- 2r^2 cos(\delta)}$$

(I see now that Vela had said essentially the same thing.)

 

[patm95]

Thanks very much for all the help. I did get this right thanks to all your help!