turnstile
- 26
- 0
Hi..
Im back
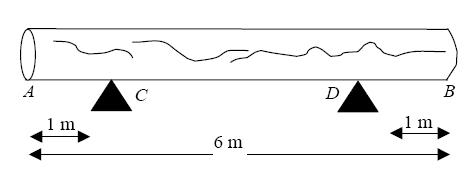
A large log AB is 6 m long. It rests in a horizontal position on two smooth supports C and D, where AC = 1 m and BD = 1 m, as shown in Figure . David needs an estimate of the weight of the log, but the log is too heavy to lift off both supports. When David applies a force of magnitude 1500 N vertically upwards to the log at A, the log is about to tilt about D.
(a) State the value of the reaction on the log at C for this case.
... 0...
David initially models the log as uniform rod. Using this model,
(b) estimate the weight of the log
[ I got 3750 N for this]
The shape of the log convinces David that his initial modelling assumption is too simple. He removes the force at A and applies a force acting vertically upwards at B. He finds that the log is about to tilt about C when this force has magnitude 1000 N. David now models the log as a non-uniform rod, with the distance of the centre of mass of the log from C as x metres. Using this model, find
(c) a new estimate for the weight of the log,
im absolutely stuck here... the way I've laid it out is;
Moments at D => 1500x5 =W(4-x)
Moments at C => 1000x5 =?
then... ?
I don't know what to do...
(d) the value of x.
Any help would be appreciated. :)
Im back
A large log AB is 6 m long. It rests in a horizontal position on two smooth supports C and D, where AC = 1 m and BD = 1 m, as shown in Figure . David needs an estimate of the weight of the log, but the log is too heavy to lift off both supports. When David applies a force of magnitude 1500 N vertically upwards to the log at A, the log is about to tilt about D.
(a) State the value of the reaction on the log at C for this case.
... 0...
David initially models the log as uniform rod. Using this model,
(b) estimate the weight of the log
[ I got 3750 N for this]
The shape of the log convinces David that his initial modelling assumption is too simple. He removes the force at A and applies a force acting vertically upwards at B. He finds that the log is about to tilt about C when this force has magnitude 1000 N. David now models the log as a non-uniform rod, with the distance of the centre of mass of the log from C as x metres. Using this model, find
(c) a new estimate for the weight of the log,
im absolutely stuck here... the way I've laid it out is;
Moments at D => 1500x5 =W(4-x)
Moments at C => 1000x5 =?
then... ?
I don't know what to do...
(d) the value of x.
Any help would be appreciated. :)
 I am not getting the answer...
I am not getting the answer...