L1988
- 11
- 0
Two questions:
1. A sailor strikes the side of his ship just below the waterline. He hears the echo of the sound reflected from the ocean floor directly below 2.02 s later. How deep is the ocean at this point?
I assumed this used distance = speed x time. I knew that speed must equal the speed of sound in water, which I think is 1500 m/s (pretty sure, but not 100%) and I also divided my final distance by 2 so that I only got the distance of depth one way. However, the computer (this is online homework) said I was wrong, so I'm not sure where I went wrong. Any help would probably help me with the next problem too.
2.
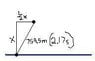
A rescue plane flies horizontally at a constant speed searching for a disabled boat. When the plane is directly above the boat, the boat's crew blows a loud horn. By the time the plane's sound detector perceives the horn's sound, the plane has traveled a distance equal to one half its altitude above the ocean. If it takes the sound 2.17 s to reach the plane, determine the altitude of the plane. Take the speed of sound to be 350 m/s.
Just like last time, I assumed that I should use
distance= speed of sound x time
with a new speed (350 m/s), new time, and this time distance doesn't have to be divided by 2. However, that got me the wrong answer.
Then I tried drawing a triangle, (since the plane has moved) and called my final distance r^2 and my x^2 = one half its altitude, so all that was left was y^2. This also was incorrect.
Where am I making a mistake?
1. A sailor strikes the side of his ship just below the waterline. He hears the echo of the sound reflected from the ocean floor directly below 2.02 s later. How deep is the ocean at this point?
I assumed this used distance = speed x time. I knew that speed must equal the speed of sound in water, which I think is 1500 m/s (pretty sure, but not 100%) and I also divided my final distance by 2 so that I only got the distance of depth one way. However, the computer (this is online homework) said I was wrong, so I'm not sure where I went wrong. Any help would probably help me with the next problem too.
2.
A rescue plane flies horizontally at a constant speed searching for a disabled boat. When the plane is directly above the boat, the boat's crew blows a loud horn. By the time the plane's sound detector perceives the horn's sound, the plane has traveled a distance equal to one half its altitude above the ocean. If it takes the sound 2.17 s to reach the plane, determine the altitude of the plane. Take the speed of sound to be 350 m/s.
Just like last time, I assumed that I should use
distance= speed of sound x time
with a new speed (350 m/s), new time, and this time distance doesn't have to be divided by 2. However, that got me the wrong answer.
Then I tried drawing a triangle, (since the plane has moved) and called my final distance r^2 and my x^2 = one half its altitude, so all that was left was y^2. This also was incorrect.
Where am I making a mistake?
Last edited: