How Can I Accurately Determine the Critical Angle in an Unknown Material?

[dykuma]

Homework Statement

An electromagnetic wave is incident into the flat surface of an unknown material. In the surface, the transverse wave mode follows the relation $\omega^2 = \omega_m + c^2 k^2$ , where $\omega_m$ is an angular frequency associated with the material. The angular frequency of the incident wave is $\omega = 2 \omega_m$

What is the incident wavelength and the transverse wavelength in terms of the speed of light and the angular frequency associated with the material? Then, determine the critical angle such that there is no transmission into the material?

Relevant Equations

I'm expecting to use snell's law, as well as equations related to wave numbers and the index's of refraction.

First, I attempted to find the wavelength of the incident wave in the required terms:

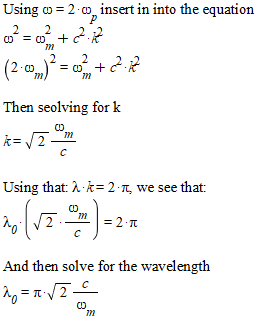
Next, I tried to find the wavelength inside of the material:

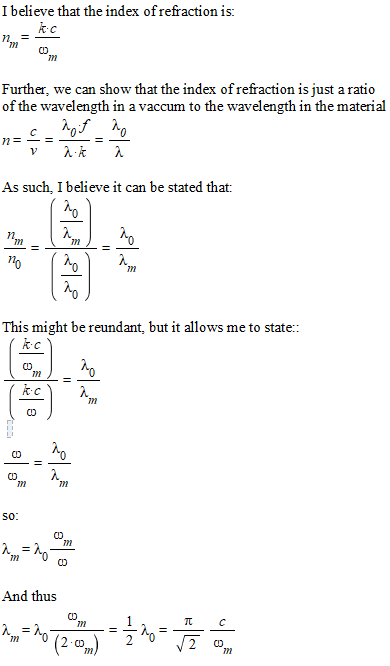
And then lasted, I tried to find the critical angle:

My issue is that
1) I don't know if what I did was correct.
2) I don't think what I did was correct because that angle is in the complex plane. Maybe this unknown material is wild stuff, but I'm not sure that is possible. If I invert the answer, (that is, assume that I did the problem backwards and mixed up the wavelengths),I get a critical angle of pi/6, which is almost too nice not to be the right answer.

Anyway, any help or direction on this problem would be appreciated.

 

[mark726]

Thank you for sharing your attempts at finding the wavelength and critical angle in the unknown material. I would like to provide some guidance and clarification on your approach.

Firstly, to find the wavelength of the incident wave in the required terms, you can use the formula λ = c/f, where c is the speed of light and f is the frequency of the wave. If you have the frequency in the required terms, you can simply plug it into the formula to find the wavelength.

Next, to find the wavelength inside the material, you can use the formula λ = λ₀/n, where λ₀ is the wavelength in vacuum and n is the refractive index of the material. If you have the refractive index in the required terms, you can use it to find the wavelength inside the material.

Lastly, to find the critical angle, you can use the formula sinθc = n₂/n₁, where n₂ is the refractive index of the second medium (in this case, the unknown material) and n₁ is the refractive index of the first medium (usually air or vacuum). This angle is not in the complex plane, but rather in the real plane. If you are getting a value in the complex plane, it could be due to an error in your calculations.

In conclusion, your approach to finding the wavelength and critical angle is correct, but it is important to double-check your calculations and ensure that the values you are using are in the correct terms. If you are still unsure about your answers, I recommend consulting with a colleague or seeking additional resources for assistance.

I hope this helps and good luck with your research!