flanders
- 10
- 0
Homework Statement
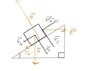
Hi. My task is to find the Force F, so that velocity is constant.
I know that the velocity is constant, therefore the sum of all forces must be zero!
On the image I have used vector decomposition (the black lines). The orange ones are the vectors.
I know that the angle is 36,9 degrees. (the one marked with a half a circle).
I also know that the friction number is 0,25.
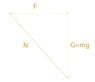
Explanation of the attached image:
G = Gravity
N = Normal Force
Ff = Friction
F = The force I must find
Homework Equations
Gx=0,6mg
Gy=0,8mg
Fx=0,8ma
Fy=0,6ma
\mu \; =\; 0.25
N = Gy + Fy
The Attempt at a Solution
I have tried to find N by using this formula:
\mu \; =\; \frac{Ff}{N}
Then I thought that I could find Fy and Fx and use Phytagoras to find F. But my idea doesn't work (at least not the way I did it).
I don't know how to think to solve this one... The mass is unknown and frustrates me a lot. Can anyone give me a tip?
Attachments
Last edited: