- #1
andreass
- 16
- 0
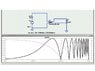
Here's the thing. I have 4,7 nF capacitor and AC: 1 kHz < f < 10 MHz.
I measure real and imaginary part of capacitance C*=C'+iC" (C'=C'(f) and C"=C"(f)).
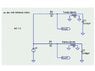
I did 2 measurements - in first capacitor is directly attached to measuring device, in second I use 1 m coaxial cables to attach it.
I need to get impedance per length for cables.
1. How can I get absolute value of impedance??
1.) |C| = sqrt(C'^2+C"^2) and |Z| = 1/|C|/(2*pi*f) or
2.) Z = 1/(2*pi*f*C*) = (C"-iC')/(2*pi*f*(C'+C")) and |Z| = sqrt(C'^2+C"^2)/(2*pi*f*(C'+C"))
And then, I assume, I can subtract absolute value of |Z| for first and second measurement and I should get impedance per meter for my cables !??
I measure real and imaginary part of capacitance C*=C'+iC" (C'=C'(f) and C"=C"(f)).
I did 2 measurements - in first capacitor is directly attached to measuring device, in second I use 1 m coaxial cables to attach it.
I need to get impedance per length for cables.
1. How can I get absolute value of impedance??
1.) |C| = sqrt(C'^2+C"^2) and |Z| = 1/|C|/(2*pi*f) or
2.) Z = 1/(2*pi*f*C*) = (C"-iC')/(2*pi*f*(C'+C")) and |Z| = sqrt(C'^2+C"^2)/(2*pi*f*(C'+C"))
And then, I assume, I can subtract absolute value of |Z| for first and second measurement and I should get impedance per meter for my cables !??