Unable to get the desired impedance in this LTspice simulation

[brainbaby]

TL;DR Summary

Impedance matching

Hello friends,

I am studying an article on impedance matching which states about matching a resistance of 52 ohms with 2k ohm. It is accomplished by adding an inductance of XL= 318 ohms in series with the 52 ohm resistor yielding a parallel equivalent of 328ohm as reactance and 2k ohm as my desired resistance. see in fig 1.

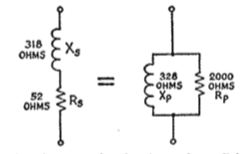
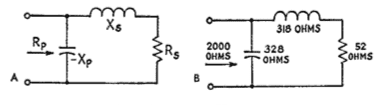
fig 2 states adding a counter reactance to negate the additional reactance as in fig 1 part 2...(leaving it for a moment)

I simulated this circuit in LTspice and found out the impedance to be 1Meg ohms which way beyond my expectation of 2k ohm.
(I have tried many arbitrary values of f and L and haven't found any luck yet. For the time being its 5H.)
I am not sure about what inductance value should I take so that I can achieve resultant impedance of 2k ohm in the graph.
Unfortunately I also don't have the frequency value as it is not mentioned in the article.(XL=2.pi.f.L)

What inductance and f should be need for 2k ohm as a result.?

Thank you!

 

[berkeman]

Summary:: Impedance matching

Unfortunately I also don't have the frequency value as it is not mentioned in the article.(XL=2.pi.f.L)

What inductance and f should be need for 2k ohm as a result.?

Write the equations for the two complex impedances and solve them for those unknowns? Are you trying to use the same inductance in both circuits? If not, you will have 3 unknowns and 2 equations...

 

[tech99]

Write the equations for the two complex impedances and solve them for those unknowns? Are you trying to use the same inductance in both circuits? If not, you will have 3 unknowns and 2 equations...

There is only one circuit I think. The values look about right using approximations with mental arithmetic:-
1) Transformation ratio, N = 2000/50 = 40
2) Required Q = sqrt N = sqrt 40 = 6.5
3) Xc = XL = Q * 50 = 325 ohms

 

[berkeman]

There is only one circuit I think.

I was referring to these two, but maybe I'm not understanding the problem statement...

 

[tech99]

I was referring to these two, but maybe I'm not understanding the problem statement...

View attachment 257013

OK yes I see.

 

[brainbaby]

Are you trying to use the same inductance in both circuits?

They are not two different circuits.
The second one is just a parallel equivalent of the initial one.

Write the equations for the two complex impedances and solve them for those unknowns

I am having two unknowns. All I have is the reactance value i.e 318 ohm. It left me with an unknown freq. and inductance (L).

 

[brainbaby]

There is only one circuit I think

Absolutely.

 

[brainbaby]

I'm not understanding the problem statement

With two unknowns how can I able to find value of L (on simulation as well)

 

[berkeman]

They are not two different circuits.
The second one is just a parallel equivalent of the initial one.

No. There is no way to make these two circuits equivalent across a range of frequencies. You should be able to match their complex impedance at a single frequency, I think, but I haven't tried it yet.

 

[brainbaby]

There is no way to make these two circuits equivalent across a range of frequencies. You should be able to match their complex impedance at a single frequency,

yes. I agree but I can't find the freq until I know the inductance.

 

[Joshy]

Matching network chapters in my textbooks talk about something similar... series to parallel equivalent circuits, but what it's trying to show is that the impedance is stepped up or down by about $Q^2$ (assuming Q >> 1)

What I think I see in the OP is an attempt to use the series to parallel equivalent circuit as a matching network, but it is not a matching network. How to see what I think you're looking for? I would recommend doing a frequency (AC) sweep; plot values from the voltage source instead of other elements. Here:

The Q of the series one with the 318 Ohm inductor and 52 Ohm resistor is about 6.115. This is not much greater than one so the $Q^2$ approximation won't work very well, but that was based off of

$$R_s = {{R_p} \over {1 + Q^2}}$$

So you'll see it'll get to about 52 Ohms.

$$52.086 = {{2000} \over {1 + 6.11538^2}}$$

Higher Q correlates to narrow band. After it talks about all that fun stuff, then it'll talk about a L network. If the OP wants to match a 52 Ohm load to a 2000 Ohm source, then they can do something that'll look like series L and shunt C away from the load (followed by the source impedance). I would recommend reading about Smith charts rather than doing the calculation by hand... even though it's more common for RF engineering... the math still works and it's much more convenient and fun than the hand calculations (you could actually eye ball the values and get really close).

Solve for the reactive values and you'll be done so far as how your literature is doing it; you can choose a frequency after because you know that $X_L$ is $\omega L$ and $X_C$ is ${1} \over {\omega C}$.

 

[Baluncore]

A Pi filter can be used to match a narrow band. Wider bands can be matched by ladder networks with multiple stages. The Pi topology can be either low or high pass. You must specify the terminal impedances, frequency, and Q.
You can also use L or T networks.
There is a calculator here; https://www.eeweb.com/tools/pi-match
Attached is an LTspice model Pi for freq = 1kHz with Q=20.

 

[Tom.G]

Summary:: Impedance matching

I am not sure about what inductance value should I take so that I can achieve resultant impedance of 2k ohm in the graph.
Unfortunately I also don't have the frequency value as it is not mentioned in the article.(XL=2.pi.f.L)

The article is stating that to match 52Ω to 2000Ω you will need a an inductive reactance of 318Ω and a capacitive reactance of 328Ω. You choose the parts values, inductance and capacitance, to get those reactances at whatever frequency you are operating at. If you want to operate at a different frequency, you must choose different component values to obtain the needed reactances.

So choose a frequency, then compute what inductance and capacitance values you need that have the required reactances.

For further understanding, find the L and C values for 1/2 the frequency, twice the frequency, 10 times the frequency.

Cheers,
Tom

 

[sophiecentaur]

Summary:: Impedance matching

Unfortunately I also don't have the frequency value as it is not mentioned in the article.

This is a very popular topic. Why not locate a different article in which all the variables are actually stated. This lacking piece of information is causing far more angst that is really necessary.

 

[Joshy]

It may throw some off, but the OP doesn't need the frequency to solve the problem. They only need to solve for the reactive values. These values will be the same no matter frequency they are solving at.

This is just a L network. The problem is solved- good for all frequencies (results are normalized by 2000). L networks are great for learning. I would recommend trying that one first. Read about Smith charts and you'll be able to "see" the answers without any tedious calculations just like above.

$x_L = 0.016$ and ${1 \over | x_C|} = 6.1$

Now: If they want to solve for specific L and C values, then they will need the frequency, but it doesn't change the above. Example simulated below you'll see the match no matter which frequency I plug into the parametric sweep.