How can I know when to use different trigonometric functions?

[ann]

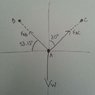
Can someone please explain to me why in this problem, for example, the sine and cosine functions are used in equating the force's components? I am having a hard time solving for these unknown forces because of my rusty trig skills.

It asks to "determine the maximum weight of the flowerpot that can be supported without exceeding a cable tension of 50lb in either cable AB or AC." My professor provided these calculations:
∑Fx=0
F_AC*sin(30)-F_AB*cos(53.13)=0
50*sin(30)-F_AB*cos(53.13)=0
F_AB=41.66lb

∑Fy=0
F_AC*cos(30)+F_AB*sin(53.13)-W=0
50*cos(30)+41.66*sin(53.13)-W=0
W=76.63 lb

Why did they use the sine and cosine functions for this specific problem. Where they used the sine function, for example, why couldn't they have used a tangent function instead?

 

[SteamKing]

You should also review what the sine and cosine of an acute angle mean:

http://en.wikipedia.org/wiki/Trigonometry

It helps to complete the triangles when trying to decide which trig function to use.

For the example in the OP, draw a horizontal line from C perpendicular to the vertical axis.

Draw a vertical line from B perpendicular to the horizontal axis.

What you want to do is calculate the horizontal and vertical components of the tensions in lines AB and AC.
You use these components to establish the static equilibrium of the flower pot.

The tangent function has virtually no use in computing components, unless you are dealing with friction.