How can I model a density function of a compressible fluid?

[Se Adolf]

I have a cylinder of some dimensions. I have a compressible liquid inside. Assuming a constant temperature, no atmosphere, no convection currents within, because it is in a cylinder, there will be no variations in density horizontally (the fluid will have time to settle). Now because there is gravity, the liquid will be pulled down and because the volume of water on top increases as depth increases, the fluid will be more dense at the bottom than at the top. So I pick for example two densities: 0.5 and 1 with 0.5 at the very top of the cylinder and 1 at the very base of it. Something as follows:

https://ibb.co/DCWmTZH

https://ibb.co/DCWmTZH < Sloppy Diagram of what I mean

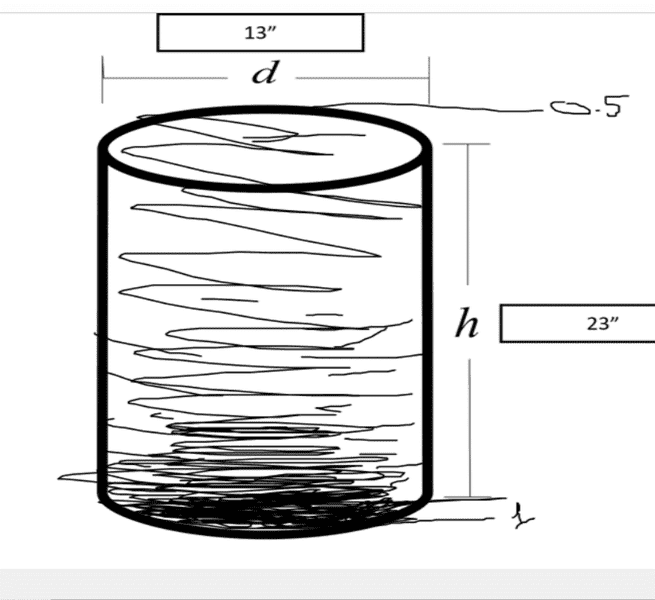
So my question is how can I model this? How can I get some kind of density function out of this? Please go easy on me, I don't really do physics, this is for a Mathematics investigation. Thank you in advance for help, I'm kinda desperate at this point :P.

 

[BvU]

Hello Se Adolf,

Perhaps you can find some inspiration in the derivation of the barometric formula ?

 

[Chestermiller]

For a liquid, the density can be approximated by $$\rho=\rho_0[1+\beta (P-P_0)]$$where $\rho_0$ is the liquid density at pressure $P_0$, P is the local pressure in the liquid, and $\beta$ is the bulk compressibility of the liquid.

The liquid in the cylinder is under hydrostatic conditions, so the pressure is related to elevation z above the bottom of the cylinder by $$\frac{dP}{dz}=-\rho g$$If we combine these two equations, we obtain: $$\frac{dP}{dz}=-\rho_0 g[1+\beta (P-P_0)]$$If we solve this equation for the pressure P as a function of the elevation z, we obtain:
$$P=P_Be^{-\rho_{0} g \beta z}+\left[P_0-\frac{1}{\beta}\right](1-e^{-\rho_{0} g \beta z})$$
where $P_B$ is the pressure at the base of the cylinder z = 0.

Once the pressure at the base is specified, we can determine the pressure at any elevation in the cylinder. We can also integrate this equation over the height of the cylinder to get the average pressure, and also the average liquid density.