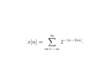Boltzman Oscillation
- 233
- 26
Homework Statement
Prove the discreet signal is periodic:
Homework Equations
for periodic funtions: x[n] = x[n + N]
The Attempt at a Solution
I made an equality (im going to leave the sigma out for simplicity):
2^(-abs(n-2m)) = 2^(-abs(n+N-2m))
I don't know what I need to do from here. The absolute value throws me off, I don't know what to do with it. My guess would be that the only thing that matters is what is inside the abs since everything else is the same so I really only need for the follwing to be true:
abs(n-2m) = abs(n+N-2m)..........(1)
but then N = 0
I guess I could make N = (-2n +4m) since using this in equation (1) will get me:
abs(n-2m) = abs(-n+2m) = abs(-(n-2m)) which is true. Then N can equal (-2n + 4m). Now doesn't N have to be independent of n? Did I do this right? I sort of started getting the idea as I went along here so sorry if I solved it.