rayhan619
- 75
- 0
Homework Statement
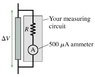
A circuit you're building needs a voltmeter that goes from 0 to a full-scale reading of 5.0 V. Unfortunately, the only meter in the storeroom is an ammeter that goes from 0 to a full-scale reading of 500 microA. It is possible to use this meter to measure voltages by putting in a measuring circuit as shown in the figure. (Figure attached)
What value of R must you use so that the meter will go to full scale when the potential difference Delta V is 5.0 V? Assume that the ammeter is ideal.
Homework Equations
I = VR