How did the author determine the range of x for this problem?

[moaath]

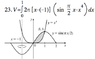
y=x^4, y=sin(pix/2); about x=-1

the solution is attached .

how he determinate it to be from 0 to 1 ...?
as I know , we usually put for example the expression of y1 = y2 and solve it for zero but in this case is not easy to do it,so how did he do it...??







note: my english is bad so please correct any thing wrong in my writing...thanks.

 

[Astronuc]

y=x^4, y=sin(pix/2) intersect at 0 and 1, and looking at the shaded area in the figure, that is the area bounded (between) the two curves (function).

 

[moaath]

may you show me the procedure of equaling the two equations step by step

thanks

 

[Mark44]

how he determinate it to be from 0 to 1 ...?
as I know , we usually put for example the expression of y1 = y2 and solve it for zero but in this case is not easy to do it,so how did he do it...??

You're right about the difficulty of solving an equation such as sin(pi * x/2) = x^4. Equations like this, where x appears in the argument of a transcendental function and outside it, are usually impossible to solve by algebraic means. I suspect that the author of this problem cooked up these functions so they would intersect at the origin and (1, 1).