moaath
- 6
- 0
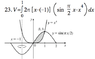
y=x^4, y=sin(pix/2); about x=-1
the solution is attached .
how he determinate it to be from 0 to 1 ...?
as I know , we usually put for example the expression of y1 = y2 and solve it for zero but in this case is not easy to do it,so how did he do it...??
note: my english is bad so please correct any thing wrong in my writing...thanks.
the solution is attached .
how he determinate it to be from 0 to 1 ...?
as I know , we usually put for example the expression of y1 = y2 and solve it for zero but in this case is not easy to do it,so how did he do it...??
note: my english is bad so please correct any thing wrong in my writing...thanks.